Eckhardt, A. K.; Schreiner, P. R., Angew. Chem. Int. Ed. 2018, 57, 5248-5252
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission
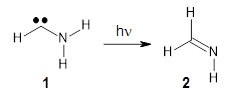
 '
'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission
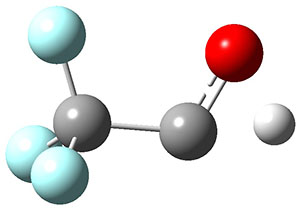
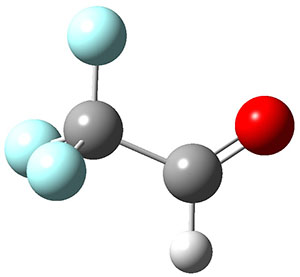
Eckhardt and Schreiner have spectroscopically characterized the aminomethylene carbene 1.1 Their characterization rests on IR spectra, with comparison to the computed AE-CCSD(T)/cc-pCVQZ anharmonic vibrational frequencies, and the UV-Vis spectra, with comparison to the computed B3LYP/6–311++G(2d,2p) transitions.
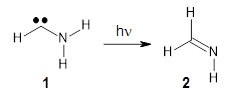
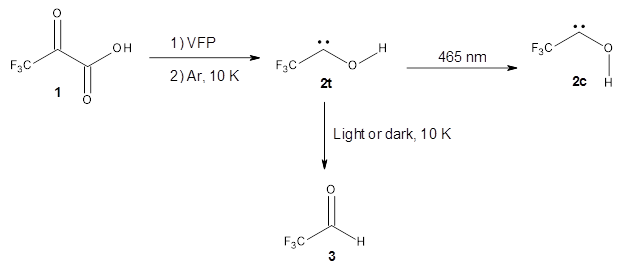
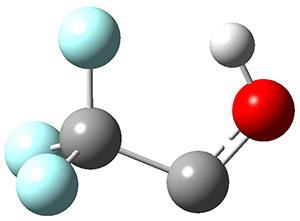
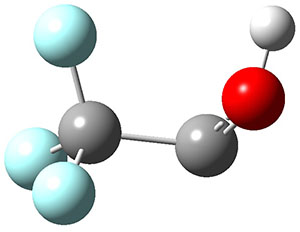
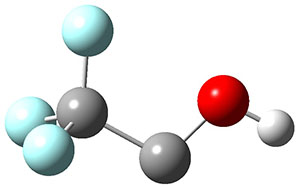
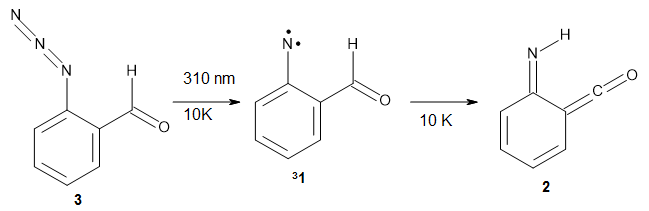
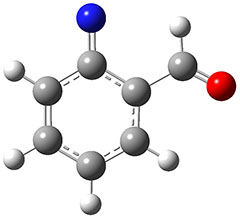
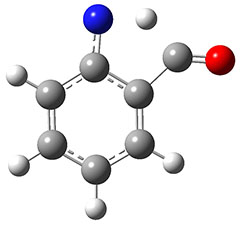
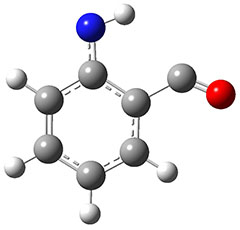
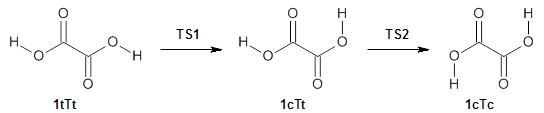
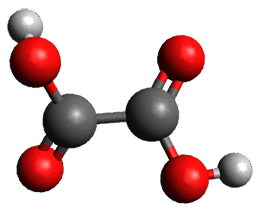
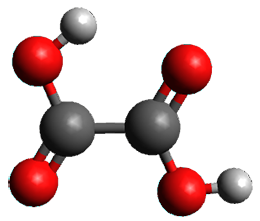
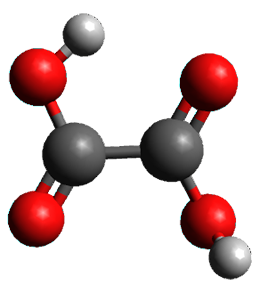
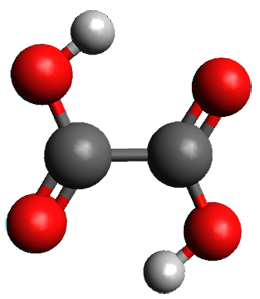
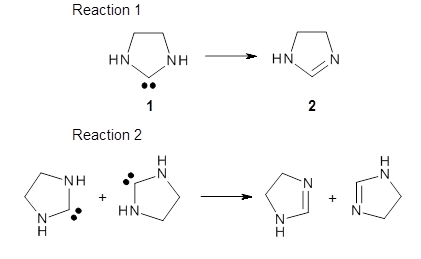
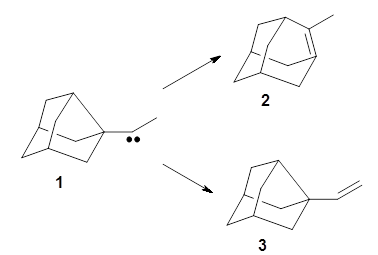
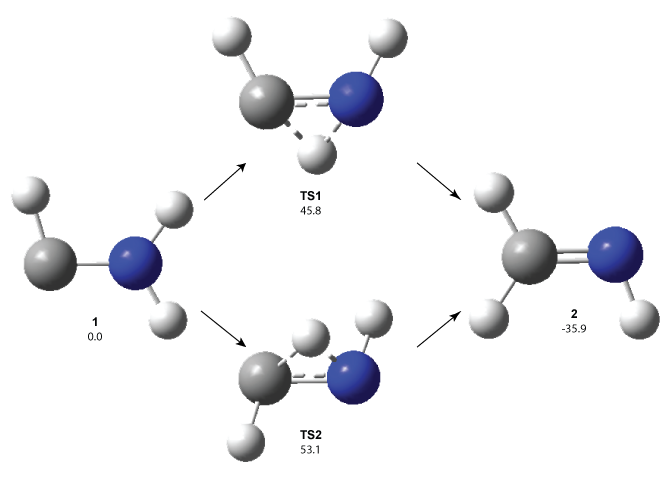
1 can be converted to 2 by photolysis. Interestingly, 1 does not convert to 2 after 5 days on the matrix in the dark. This is in distinct contrast to hydroxycarbene and related other carbene which undergo quantum mechanical tunneling (see this post and this post). Examination of the potential energy surface for the reaction of 1 to 2 at AE-CCSD(T)/cc-pCVQZ (see Figure 1) identifies that the lowest barrier is 45.8 kcal mol-1, about 15 kcal mol-1 larger than the barrier for the hydroxycarbene rearrangement. Additionally, the barrier width for 1 → 2 is 25% larger than for the hydroxycarbenes. Both of these suggest substantially reduced tunneling, and WKB analysis predicts a tunneling half-life of more than a billion years. The stability of 1 is attributed to the strong π-donor ability of nitrogen to the electron-poor carbene. This is reflected in a very short C-N bond (1.27 Å).

Figure 1. Structures and energies of 1 and 2 and the transition states that connect them. The relative energies (kcal mol-1) are computed at AE-CCSD(T)/cc-pCVQZ.
References
1) Eckhardt, A. K.; Schreiner, P. R., "Spectroscopic Evidence for Aminomethylene (H−C̈−NH2)—The
Simplest Amino Carbene." Angew. Chem. Int. Ed. 2018, 57, 5248-5252, DOI: 10.1002/anie.201800679.
Simplest Amino Carbene." Angew. Chem. Int. Ed. 2018, 57, 5248-5252, DOI: 10.1002/anie.201800679.
InChIs
1: InChI=1S/CH3N/c1-2/h1H,2H2
InChIKey=KASBEVXLSPWGFS-UHFFFAOYSA-N
InChIKey=KASBEVXLSPWGFS-UHFFFAOYSA-N
2: InChI=1S/CH3N/c1-2/h2H,1H2
InChIKey=WDWDWGRYHDPSDS-UHFFFAOYSA-N
InChIKey=WDWDWGRYHDPSDS-UHFFFAOYSA-N
 '
'This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.