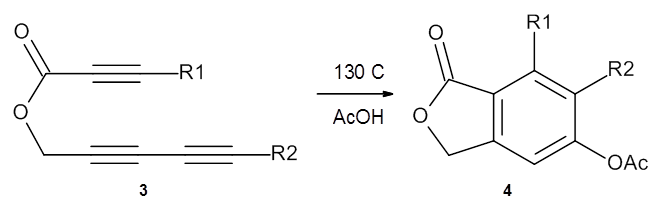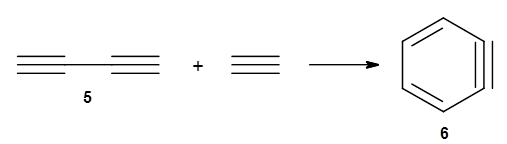Reproducing Reaction Mechanisms with Machine Learning Models Trained on a Large-Scale Mechanistic Dataset

Joonyoung F. Joung, Mun Hong Fong, Jihye Roh, Zhengkai Tu, John Bradshaw, and Connor Wilson Coley (2024)
Highlighted by Jan Jensen

Figure 1 from the paper. (c) the authors 2024

If you don't follow this particular subject, you might be surprised to learn that there isn't a large database of elementary reactions relevant to organic synthesis. Until now. 

While datasets such as Reaxys contain millions of reactions, they are typically multistep reactions. That's mostly fine for training retrosynthesis algorithms (although the authors present discuss some disadvantages), but presents a challenge if you want to use more physically based methods such as QM to predict reactivity. For example, while there are some databases of transition states (TSs) they are typically for synthetically irrelevant reactions. So, for example, while very promising methods have been developed for TS prediction, they have been trained on these datasets and are thus have limited practical applicability to synthesis.

This paper is an important step towards fixing this:

"We  identified the most popular 86 reaction types in Pistachio and curated elementary reaction templates (Figure 1c) for each of these 86 reaction types with 175 different reaction conditions (e.g., types of mechanisms). ... By applying these expert elementary reaction templates to the reactants in Pistachio, we obtained the recorded products as well as unreported  byproducts and side  products. We systematically  selected  and  preserved  the  mechanistic  pathways leading to the formation of the recorded product for  each  entry,  resulting in a comprehensive dataset comprising 1.3 million overall reactions and 5.8 million elementary reactions."

The next step is now to use this data to obtain TSs for these elementary reactions - a difficult but important challenge to the CompChem community.

This work is licensed under a Creative Commons Attribution 4.0 International License.

TS-Tools: Rapid and Automated Localization of Transition States Based on a Textual Reaction SMILES Input

Thijs Stuyver (2024)
Highlighted by Jan Jensen

Figure 2 from the paper. (c) the author 2024 reproduced under the CC-BY-NC-ND licence

This paper caught my eye for several reasons. It's an open source implementation of Maeda's AFIR method, but modified for double-ended TS searches. The setup is completely automated and interfaced to  xTB so it is fast. It's applied to really challenging problems such as solvent assisted bimolecular reactions and uncovers some important shortcomings of the xTB method. 


This work is licensed under a Creative Commons Attribution 4.0 International License.

Accurate transition state generation with an object-aware equivariant elementary reaction diffusion model

Chenru Duan, Yuanqi Du, Haojun Jia, and Heather J. Kulik (2023)
Highlighted by Jan Jensen

Part of Figure 1 from the paper. 

As anyone who has tried it will know, finding TSs is one of the most difficult, fiddly, and frustrating tasks in computational chemistry. While there are several methods aimed at automating the process, they tend to have a mixed success rate or be computationally expensive and, often, both.

This paper looks to be an important first step in the right direction. The method produces a guess at a TS structure based on the coordinates of the reactants and products. Notably, the input structures need not be aligned or atom mapped! 

The method achieves a median RMSD of 0.08 Å compared to the true TSs and it often so good that single point energy evaluation gives a reliable barrier. The method also predicts  a confidence scoring model for uncertainty quantification, which allows you to a priori judge whether such a single point is sufficient or whether a TS search is warranted. The approach allows for accurate reaction barrier estimation (2.6 kcal/mol) with DFT  optimizations needed for only 14% of the most challenging reactions.

So, the method's not going to do away with manual TS searches entirely, but it is going to be invaluable for large scale screening studies. As the authors note, the method can likely also be adapted to the prediction of barrier heights, which could potentially be used to pre-screen  reactions on a much, much bigger scale. 

The paper is an important proof-of-concept study, but needs to be trained on much larger data sets (note that it is only trained on C, N, and O containing molecules), which are non-trivial to obtain. But the method could likely be used to obtain these data sets in an iterative fashion.



This work is licensed under a Creative Commons Attribution 4.0 International License.

Reactants, products, and transition states of elementary chemical reactions based on quantum chemistry

Colin A. Grambow, Lagnajit Pattanaik, William H. Green (2020)
Highlighted by Jan Jensen

Figure 1 from the paper. Reproduced under the CC BY-NC-ND 4.0 licence

This paper describes a new data set of DFT barrier heights for 12,000 diverse chemical reactions and should stimulate a lot of new ML studies on chemical reactivity.

The molecules are sampled from GDB-7 so they are relative small and contain only H, C, N, and O.  Each reaction is generated from a single molecule using single-ended GSM, so reactions with two reactants and two products are not represented in the data set. Other than these limitations the data set is very diverse:

The reactions span a wide range of both barriers and reaction energies (as seen in the figure above). Reactions with anywhere from 1 to 6 bond changes are represented (though there are only a handful with 6) as are changes to pretty much all bond types (C-H, C-C, C-N, etc). There are only 8 reaction templates with more than 100 examples and many have only a single reaction example. So, very diverse.

Best of all the authors provide atom-mapped reaction SMILES along with the barriers and reaction energies, which makes further benchmarking, analysis, and ML-studies very easy. It will be very exciting to see this data being put to good use!


This work is licensed under a Creative Commons Attribution 4.0 International License.

Semiautomated Transition State Localization for Organometallic Complexes with Semiempirical Quantum Chemical Methods

Sebastian Dohm, Markus Bursch, Andreas Hansen, Stefan Grimme (2020)

Highlighted by Jan Jensen

Automated and efficient TS searches is difficult and there are only a few benchmark studies out there. But this is the first paper I have come across where they attempt this for organometallics. Given the typical size of organometallic compounds, one needs something faster than DFT for efficiency so semiempirical QM (SQM) methods are the obvious choice as long as these simpler methods can describe the chemistry accurately.

The authors have test MOPAC and xTB interfaces to Zimmerman's growing string method (mGSM) on the 34 unimolecular reactions in the MOBH35 benchmark set. I couldn't find an explanation for the focus on unimolecular reactions but the reason might be that it is easier to geometrically align reactants and products for these reactions.

GFN1-xTB and GFN2-xTB find reaction paths for 31 and 30 reactions, respectively, while the corresponding numbers for PM6-D3H4 and PM7 are 26 and 25, respectively. GFN2-xTB fails to find barriers for 2 reactions with < 1.5 kcal/mol barriers, so if these are discounted then GFN2-xTB performs best. 

The TS-guess structures (the highest energy point on the reaction paths) are generally in good agreement with DFT, with heavy atom RMSDs of >0.3Å. It would have been interesting to know how many DFT TS searchers converge starting from the SQM structures. The xTB barrier heights compare reasonably well with DFT, with a MAD of 8-9 kcal/mol. 

This work is licensed under a Creative Commons Attribution 4.0 International License.

Ambimodal Trispericyclic Transition State and Dynamic Control of Periselectivity

Xue, X.-S.; Jamieson, C. S.; Garcia-Borràs, M.; Dong, X.; Yang, Z.; Houk, K. N., J. Am. Chem. Soc. 2019, 141, 1217
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

A major topic of this blog has been the growing body of studies that demonstrate that dynamic effects can control reaction products (see these posts). Often these examples crop up with valley ridge inflection points. Another cause can be bispericyclic transition states, first discovered by Caramello et al for the dimerization of cyclopentadiene.¹ The Houk group now reports on the first trispericyclic transition state.²

Using ωB97X-D/6-31G(d), they examined the reaction of the tropone derivative 1 with dimethylfulvene 2. Three possible products can arrive from different pericyclic reactions: 3, the [4+6] product; 4, the [6+4] product; and 5, the [8+2] product. The thermodynamic product is predicted to be 5, but it is only 1.2 kcal mol^-1 lower in energy than 4 and 6.2 kcal mol^-1 lower than 3.

They identified one transition state originating from the reactants TS1. Hypothesizing that it would be trispericyclic, they performed a molecular dynamics study with trajectories starting from TS1. They ran a total of 142 trajectories, and 87% led to 3, 3% led to 4, and 3% led to 5. This demonstrates the unusual nature of TS1 and the dynamic effects on this reaction surface.

TS1
TS2	TS3

Figure 1. ωB97X-D/6-31G(d) optimized geometries of TS1-TS3.

Additionally, there are two different Cope rearrangements (through TS2 and TS3) that convert 3 into 4 and 5. Some trajectories can pass from TS1 and then directly through either TS2 or TS3 and these give rise to products 4 and 5. In other words, some trajectories will pass from a trispericyclic transition state and then through a bispericyclic transition state before ending in product.

References

1. Caramella, P.; Quadrelli, P.; Toma, L., “An Unexpected Bispericyclic Transition Structure Leading to 4+2 and 2+4 Cycloadducts in the Endo Dimerization of Cyclopentadiene.” J. Am. Chem. Soc. 2002, 124, 1130-1131, DOI: 10.1021/ja016622h

2. Xue, X.-S.; Jamieson, C. S.; Garcia-Borràs, M.; Dong, X.; Yang, Z.; Houk, K. N., “Ambimodal Trispericyclic Transition State and Dynamic Control of Periselectivity.” J. Am. Chem. Soc. 2019, 141, 1217-1221, DOI: 10.1021/jacs.8b12674.

InChIs

1: InChI=1S/C10H6N2/c11-7-10(8-12)9-5-3-1-2-4-6-9/h1-6H
InChIKey=KAWLLELUFONBGI-UHFFFAOYSA-N

2: InChI=1S/C8H10/c1-7(2)8-5-3-4-6-8/h3-6H,1-2H3
InChIKey=WXACXMWYHXOSIX-UHFFFAOYSA-N

3: InChI=1S/C18H16N2/c1-11(2)17-15-7-8-16(17)14-6-4-3-5-13(15)18(14)12(9-19)10-20/h3-8,13-16H,1-2H3
InChIKey=DRPXVBLNTKGMTB-UHFFFAOYSA-N

4: InChI=1S/C18H16N2/c1-18(2)13-6-8-14(12(10-19)11-20)15(9-7-13)16-4-3-5-17(16)18/h3-9,13,15-16H,1-2H3
InChIKey=FSIPGNLAWKVXDD-UHFFFAOYSA-N

5: InChI=1S/C18H16N2/c1-12(2)13-8-9-16-17(13)14-6-4-3-5-7-15(14)18(16,10-19)11-20/h3-9,14,16-17H,1-2H3/t14?,16-,17-/m1/s1
InChIKey=SYLWEGLODFLARZ-VNCLPFQGSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Artificial Intelligence Assists Discovery of Reaction Coordinates and Mechanisms from Molecular Dynamics Simulations

Hendrik Jung, Roberto Covino, and Gerhard Hummer. arXiv: 1901.04595

Contributed by Jesper Madsen

Here, I highlight a recent preprint describing an application of Artificial Intelligence/Machine Learning (AI/ML) methods to problems in computational chemistry and physics. The group previously published the intrinsic map dynamics (iMapD) method, which I also highlighted here on Computational Chemistry Highlights. The basic idea in the previous study was to use an automated trajectory-based approach (as opposed to a collective variable-based approach) to explore the free-energy surface a computationally expensive Hamiltonian that describes a complex biochemical system.

Fig 1: Schematic flow chart of the AI-assisted MD simulation algorithm.

The innovation in their current approach is the combination of the sampling scheme, statistical inference, and deep learning to construct a framework where sampling and mechanistic interpretation happens simultaneously – an important milestone towards completely “autonomous production and interpretation of MD simulations of rare events,” as the authors themselves remark.

It is reassuring to see that the method correctly identifies known results for benchmark cases (the alanine dipeptide and LiCl dissociation) and out-competes traditional approaches such as transition path sampling in terms of efficiency. In these simple model cases, however, complexity is relatively low and sampling is cheap. I will be looking forward to seeing the method applied to a much more complex problem in the future; E.g. a problem where ergodicity is a major issue other challenges, such as hysteresis, plays a significant role.

Another much appreciated aspect of general interest in this paper that I am emphasizing is the practical approach to interpretation of the constructed neural networks. All in all, there are many useful comments and observations in this preprint and I would recommend reading it thoroughly for those who seek to use modern AI-based methods on molecular simulations.

Computationally Augmented Retrosynthesis: Total Synthesis of Paspaline A and Emindole PB

Daria E. Kim, Joshua E. Zweig and Timothy R. Newhouse (2018)

Highlighted by Jan Jensen

Figure 2 from the paper reproduced under the CC-BY-NC-ND licence

This paper presents a rare example of using quantum chemical TS calculations to guide, rather than post-rationalise, organic synthesis. The authors wanted to design a retrosynthetic path that could be used to make two related natural products, paspaline A and emindole PB, that require either a ring closure (paspaline A) or a methyl shift (emindole PB). Three different routes were possible that lead to different functionalities that were relatively distant from the ring closure/methyl shift, which made it hard to predict the best route by chemical intuition.

Instead the authors used mPW1PW91/6-31+G(d,p)//B3LYP/6-31G(d) to find the TSs for both reactions for each of the three routes to predict the best route, which turns out to be "C". Route C did indeed work great in practice, while route A (predicted to be worst route) didn't give the desired results.

My guess is that the key here is that the synthetic question was reduced to a question of relative barrier heights of closely related reactions, i.e. ΔΔΔG^‡ = ΔΔG^‡(4→5) - ΔΔG^‡(4→6), which leads to maximum error cancellation. I hope this paper will lead to more use of QM to guide synthetic decisions and more work on making TS calculations even more accessible to synthetic chemists


This work is licensed under a Creative Commons Attribution 4.0 International License.

Automated Transition State Theory Calculations for High-Throughput Kinetics

Pierre L. Bhoorasingh, Belinda L. Slakman, Fariba Seyedzadeh Khanshan, Jason Y. Cain, and Richard H. West (2017)
Highlighted by Jan Jensen

Figure 1 from Bhoorasingh et al. J. Phys. Chem. A 2017, 121, 6896. 

Copyright 2017 American Chemical Society

I have written about automated transition state searching before, so I was interested to see how this work differed. Both methods aim at obtaining the best possible guess of the TS structure, which is then used as a starting point for a conventionional TS optimization. In the current work this is done by estimating bond lengths between the reacting atoms using a group contribution method based on known TS structures. These distances are then constrained while a conformational search is performed for the rest of the molecular structure using the UFF force field. The method is described in more detail here.

This approach is thus not too different from the TS template structure approach used in the Schrödinger study, but goes on to perform a conformational search for the TS, which the Schrödinger study did not. So it indeed encouraging to see that the conformational search seems to work and give reasonable results.

Both approaches requires that the atom orders are the same in the reactants and products. In general this is a hard problem and the Schrödinger paper offers one approach to this. However, in the current study the products are automatically generated from the reactants using the Reaction Mechanism Generator (RMG) program in such a way (I believe) that the atom order is preserved.

So if you're interested in a particular TS the current approach is unlikely to be useful since it is rather intimately tied to the RMG program and certain types of chemical reactions. However, if you are interested in these types of chemical reactions then the approach seems quite useful since the entire process is automated and appears quite robust. 

More importantly is an important proof-of-concept of what is possible in terms of automation given a large an carefully constructed training set of chemical reactions.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Efficient prediction of reaction paths through molecular graph and reaction network analysis

Yeonjoon Kim, Jin Woo Kim, Zeehyo Kim and Woo Youn Kim (2017)

Highlighted by Jan Jensen

Figure 2 from the paper. Reproduced under the CC-BY licence.

The paper presents an interesting approach to generating the most important intermediates given reactants and products. 

1. The reactants and products are mapped to atom connectivity (AC) matrices, where the presence and absence of bonds are represented by 1's and 0's. 

2. Intermediates are then enumerated by changing the matrix elements using simple rules and constraints are employed to keep the number of intermediates manageable: the change in bonding is limited to a maximum of two per steps and only changes to bonds involving "active atoms" (atoms with different bonding in reactants and products) are considered. Identifying active atoms involves mapping reactant atoms to product atoms, using the method proposed by Floudas and co-workers.  The AC matrices are converted to SMILES strings and 3D coordinates to ensure that they correspond to chemically reasonable molecules.

3. A reaction network is then constructed by finding intermediates that best connect reactants and products by computing "chemical distances (CDs)" between AC matrices and identifying intermediates with CDs to reactant and product that are similar to the CD between the reactant and product themselves. The CDs are then used to find the shortest path to reactant and product for each intermediate to yields a minimal reaction network.

4. Finally, TSs connecting the structures in the minimal reaction are found using conventional QM methods.

The method is applied to Claisen ester condensation and Cobalt-catalyzed hydroformylation. The method is implemented in a python program called ACE-Reaction but the availability of this program is unclear.  

This work is licensed under a Creative Commons Attribution 4.0 International License.

Understanding and Breaking Scaling Relations in Single-Site Catalysis: Methane-to-methanol Conversion by Fe(IV)=O

Terry Z. H. Gani and Heather J. Kulik (2017)

Highlighted by Jan Jensen

This is the first study I have come across that locates TS structures as part of a "high-throughput" single-site catalyst design study. Furthermore, the catalyst contains iron, which is not the easiest of elements to work with computationally. 

The study locates 76 and 43 TSs for the oxo formation (TS1) and hydrogen atom transfer (HAT, TS2) steps of the catalytic cycle. These are relatively small numbers compared to high throughput studies of other properties (hence the quotation marks), but they are roughly an order of magnitude larger than the number of TSs found in typical computational study of catalysts. The number is smaller for HAT due to difficulties in locating TSs for this step.

The TSs were located using either NEB implemented in DL-FIND or Q-CHEM where initial guess structures were generated using a locally modified version of molSimplify.

The studies show that there is a good correlation between reaction energy and barrier for the HAT step (R2 = 0.99) but a poor correlation for the oxo formation (R2 = 0.50 - 0.81). The authors conclude "Overall, our work shows that LFERs can be leveraged in single-site catalyst screening only when the coordination geometry is held fixed. Reliance solely on LFERs for single-site catalysis will thus miss rich areas of chemical space accessible through scaffold distortion."

This work is licensed under a Creative Commons Attribution 4.0 International License.

An automated transition state search and its application to diverse types of organic reactions

Leif D. Jacobson, Art D. Bochevarov, Mark A. Watson, Thomas F. Hughes, David Rinaldo, Stephan Ehrlich, Thomas B. Steinbrecher, S. Vaitheeswaran, Dean M. Philipp, Mathew D. Halls, and Richard A. Friesner (2017)

Highlighted by Jan Jensen

Copyright 2017 American Chemical Society

Finding transition states remains one of the most labor intensive pursuits in computational chemistry.  While interpolation methods are becoming increasingly robust, they usually require that the atom order for reactant and product are identical (atom mapping) and can be sensitive the starting conformations and relative orientation in case of bi-molecular reactions.  Furthermore, one still has to check whether the right TS is found and formulate a strategy if it is not.  All these things to do not immediately lend themselves to automation but this paper proposes solutions for all these problems.

In particular the paper offers a very elegant solution for the atom mapping problem: bonds are broken in both reactants and products until the connectivity of the fragments are identical after which the atoms in the fragments can be easily matched. Both the comparison and atom mapping of fragments can be easily done with modern cheminformatics toolkits such as RDKit using canonical smiles and  maximum common substructure searchers (after atom order and charge has been removed).  Cases where this fails due to equivalent atoms (e.g. the hydrogens in a methylene group) can then be dealt with by searching for the solution with the lowest RSMD between reactant and product.

The study focussed on relatively small and rigid molecules and issues due to multiple conformations is left for a future publication.

This work is licensed under a Creative Commons Attribution 4.0 International License.

Mechanisms and Origins of Periselectivity of the Ambimodal [6 + 4] Cycloadditions of Tropone to Dimethylfulvene

Yu, P.; Chen, T. Q.; Yang, Z.; He, C. Q.; Patel, A.; Lam, Y.-h.; Liu, C.-Y.; Houk, K. N., J. Am. Chem. Soc. 2017, 139 (24), 8251-8258
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Bispericyclic transition states arise when two pericyclic reactions merge to a common transition state. This leads to a potential energy surface with a bifurcation such that reactions that traverse this type of transition state will head towards two different products. The classic example is the dimerization of cyclopentadiene, involving two [4+2] Diels-Alder reactions. Unusual PESs are discussed in my book and in past blog posts.

Houk and coworkers have now identified a bispericyclic transition state involving two [6+4] cycloadditions.¹ Reaching back to work Houk pursued as a graduate student with Woodward for inspiration, these authors examined the reaction of tropone 1 with dimethylfulvene 2. Each moiety can act as the diene or triene component of a [6+4] allowed cycloaddition:

The product with fulvene 2 as the 6 π-e component and tropone as the 4 π-e component [6_F+4_T] is 3, while reversing their participation in the [6_T+4_F] cycloaddition leads to 4. A variety of [4+2] reactions are also possible. All of these reactions were investigated at PCM/M06-2X/6-311+G(d,p)//B3LYP-D3/6-31G(d). The reaction leading to 3 is exothermic by 3.0 kcal mol^-1, while the reaction to 4 endothermic by 1.3 kcal mol^-1.

Interestingly, there is only one transition state that leads to both 3 and 4, the first known bispericyclic transition state for two conjoined [6+4] cycloadditions. The barrier is 27.9 kcal mol^-1. The structures of the two products and the transition state leading to them are shown in Figure 1. 3 and 4 can interconvert through a Cope transition state, also shown in Figure 1, with a barrier of 26.3 kcal mol^-1 (for 4 → 3).

3	4
TS [6+4]	TS Cope

Figure 1. B3LYP-D3/6-31G(d) optimized geometries.

Given that a single transition leads to two products, the product distribution is dependent on the molecular dynamics. A molecular dynamics simulation at B3LYP-D3/6-31G(d) with 117 trajectories indicates that 4 is formed 91% while 3 is formed only 9%. Once again, we are faced with the reality of much more complex reaction mechanisms/processes than simple models would suggest.

References

1) Yu, P.; Chen, T. Q.; Yang, Z.; He, C. Q.; Patel, A.; Lam, Y.-h.; Liu, C.-Y.; Houk, K. N., "Mechanisms and Origins of Periselectivity of the Ambimodal [6 + 4] Cycloadditions of Tropone to Dimethylfulvene." J. Am. Chem. Soc. 2017, 139 (24), 8251-8258, DOI: 10.1021/jacs.7b02966.

InChIs

1: InChI=1S/C7H6O/c8-7-5-3-1-2-4-6-7/h1-6H
InChIKey=QVWDCTQRORVHHT-UHFFFAOYSA-N

2: InChI=1S/C8H10/c1-7(2)8-5-3-4-6-8/h3-6H,1-2H3
InChIKey=WXACXMWYHXOSIX-UHFFFAOYSA-N

3:InChI=1S/C15H16O/c1-15(2)10-6-8-12(14(16)9-7-10)11-4-3-5-13(11)15/h3-12H,1-2H3
InChIKey=SEKRUGIZAIQCDA-UHFFFAOYSA-N

4: InChI=1S/C15H16O/c1-9(2)14-10-7-8-11(14)13-6-4-3-5-12(10)15(13)16/h3-8,10-13H,1-2H3
InChIKey=AQQAMUGJSGJKLC-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

A few review articles

Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

A few nice review/opinion pieces have been piling up in my folder of papers of interest for this Blog. So, this post provides a short summary of a number of review articles that computationally-oriented chemists may find of interest.

Holy Grails in computational chemistry

Houk and Liu present a short list of “Holy Grails” in computationally chemistry.¹ They begin by pointing out a few technical innovations that must occur for the Grails to be found: development of a universal density functional; an accurate, generic force field; improved sampling for MD; and dealing with the combinatorial explosion with regards to conformations and configurations. Their list of Grails includes predicting crystal structures and structure of amorphous materials, catalyst design, reaction design, and device design. These Grails overlap with the challenges I laid out in my similarly-themed article in 2014.²

Post-transition state bifurcations and dynamics

Hare and Tantillo review the current understanding of post-transition state bifurcations (PTSB).³ This type of potential energy surface has been the subject of much of Chapter 8 of my book and many of my blog posts. What is becoming clear is the possibility of a transition state followed by a valley-ridge inflection leads to reaction dynamics where trajectories cross a single transition state but lead to two different products. This new review updates the state-of-the-art from Houk’s review⁴ of 2008 (see this post). Mentioned are a number of studies that I have included in this Blog, along with reactions involving metals, and biochemical systems (many of these examples come from the Tantillo lab). They close with the hope that their review might “inspire future studies aimed at controlling selectivity for reactions with PTSBs” (italics theirs). I might offer that controlling selectivity in these types of dynamical systems is another chemical Grail!

The Hase group has a long review of direct dynamics simulations.⁵ They describe a number of important dynamics studies that provide important new insight to reaction mechanism, such as bimolecular S_N2 reactions (including the roundabout mechanism) and unimolecular dissociation. They write a long section on post-transition state bifurcations, and other dynamic effects that cannot be interpreted using transition state theory or RRKM. This section is a nice complement to the Tantillo review.

Benchmarking quantum chemical methods

Mata and Suhm look at our process of benchmarking computational methods.⁶ They point out the growing use of high-level quantum computations as the reference for benchmarking new methods, often with no mention of any comparison to experiment. In defense of theoreticians, they do note the paucity of useful experimental data that may exist for making suitable comparisons. They detail a long list of better practices that both experimentalists and theoreticians can take to bolster both efforts, leading to stronger computational tools that are more robust at helping to understand and discriminate difficult experimental findings.

References

1) Houk, K. N.; Liu, F., "Holy Grails for Computational Organic Chemistry and Biochemistry." Acc. Chem. Res. 2017, 50 (3), 539-543, DOI: 10.1021/acs.accounts.6b00532.

2) Bachrach, S. M., "Challenges in computational organic chemistry." WIRES: Comput. Mol. Sci. 2014, 4, 482-487, DOI: 10.1002/wcms.1185.

3) Hare, S. R.; Tantillo, D. J., "Post-transition state bifurcations gain momentum – current state of the field." Pure Appl. Chem. 2017, 89, 679-698, DOI: 0.1515/pac-2017-0104.

4) Ess, D. H.; Wheeler, S. E.; Iafe, R. G.; Xu, L.; Çelebi-Ölçüm, N.; Houk, K. N., "Bifurcations on Potential Energy Surfaces of Organic Reactions." Angew. Chem. Int. Ed. 2008, 47, 7592-7601, DOI: 10.1002/anie.200800918

5) Pratihar, S.; Ma, X.; Homayoon, Z.; Barnes, G. L.; Hase, W. L., "Direct Chemical Dynamics Simulations." J. Am. Chem. Soc. 2017, 139, 3570-3590, DOI: 10.1021/jacs.6b12017.

6) Mata, R. A.; Suhm, M. A., "Benchmarking Quantum Chemical Methods: Are We Heading in the Right Direction?" Angew. Chem. Int. Ed. 2017, ASAP, DOI: 10.1002/anie.201611308.

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Dynamic Effects Responsible for High Selectivity in a [3,3] Sigmatropic Rearrangement Featuring a Bispericyclic Transition State

Villar López, R.; Faza, O. N.; Silva López, C., J. Org. Chem. 2017, 82 (9), 4758-4765

Contributed by Steven Bacharach

Reposted from Computational Organic Chemistry with permission

Bispericyclic reactions occur when two different pericyclic reactions merge to have a single transition state. An example of this is the joining of two [3,3]-sigmatopic rearrangements of 1 that merge to have a single transition state. Lopez, Faza, and Lopez have examined the dynamics of this reaction.¹

Because of the symmetry of the species along this reaction pathway, the products of the two different rearrangements are identical, and will be formed in equal amounts, though they are produced from a single transition state with the reaction pathway bifurcating due to a valley-ridge inflection post TS.

The interesting twist that is explored here is when 1 is substituted in order to break the symmetry. The authors have examined 3x with either fluorine, chlorine, or bromine. The critical points on the reactions surface were optimized at M06-2X/Def2TZVPP. In all three cases a single bispericyclic transition state 3TS1x is found, which leads to products 4a and 4b. A second transition state 4TSx corresponds to the [3,3]-rearrangement that interconverts the two products. The structures of 1TS, 3TS1F, and 3TS1Cl are shown in Figure 1.

1TS

3TS1F

3TS1Cl

Figure 1. M06-2X/Def2TZVPP optimized geometries of 1TS, 3TS1F, and 3TS1Cl.

The halogen substitution breaks the symmetry of the reaction path. This leads to a number of important changes. First, the C₄-C₅ and C₇-C₈ distances, which are identical in 1TS, are different in the halogen cases. Interestingly, the distortions are dependent on the halogen: in 3TS1F C₄-C₅ is 0.2 Å longer than C₇-C₈, but in 3TS1Cl C₇-C₈ is much longer (by 0.65 Å) than C₄-C₅. Second, the products are no longer equivalent with the halogen substitution. Again, this is halogen dependent: 4bF is 4.0 kcal mol^-1 lower in energy than 4aF, while 4aCl is 8.2 kcal mol^-1 lower than 4bCl.

These difference manifest in very different reaction dynamics. With trajectories initiated at the first (bispericyclic) transiting state, 89% end at 4bF and 9% end at 4aF, a ratio far from unity that might be expected from both products resulting from passage through the same TS. The situation is even more extreme for the chlorine case, where all 200 trajectories end in 4aCl. This is yet another example of the role that dynamics play in reaction outcomes (see these many previous posts).

References

1) Villar López, R.; Faza, O. N.; Silva López, C., "Dynamic Effects Responsible for High Selectivity in a [3,3] Sigmatropic Rearrangement Featuring a Bispericyclic Transition State." J. Org. Chem. 2017, 82 (9), 4758-4765, DOI: 10.1021/acs.joc.7b00425.

InChIs

1: InChI=1S/C9H12/c1-3-9-6-4-8(2)5-7-9/h1-2,4-7H2
InChIKey=RRXCPJIEZVQPSZ-UHFFFAOYSA-N

2: InChI<=1S/C9H12/c1-7-4-5-8(2)9(3)6-7/h1-6H2
InChIKey=AMBNQWVPTPHADI-UHFFFAOYSA-N

3F: InChI=1S/C9H8F4/c1-3-7-5-4-6(2)8(10,11)9(7,12)13/h1-2,4-5H2
InChIKey=VZFAQFJKHDWJDN-UHFFFAOYSA-N

3Cl: InChI=1S/C9H8Cl4/c1-3-7-5-4-6(2)8(10,11)9(7,12)13/h1-2,4-5H2
InChIKey=AIVUHFMHIMNOJB-UHFFFAOYSA-N

4aF: InChI=1S/C9H8F4/c1-5-4-6(8(10)11)2-3-7(5)9(12)13/h1-4H2
InChIKey=NAUUHIHYMAOMIF-UHFFFAOYSA-N

4aCl: InChI=1S/C9H8Cl4/c1-5-4-6(8(10)11)2-3-7(5)9(12)13/h1-4H2
InChIKey=MMCKDJXQYSGQEH-UHFFFAOYSA-N

4bF: InChI=1S/C9H8F4/c1-5-4-6(2)8(10,11)9(12,13)7(5)3/h1-4H2
InChIKey=LMFNAIRCNARWSX-UHFFFAOYSA-N

4bCl: InChI=1S/C9H8Cl4/c1-5-4-6(2)8(10,11)9(12,13)7(5)3/h1-4H2
InChIKey=NOFFASDSCUGRTP-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Cheap but accurate calculation of chemical reaction rate constants from ab initio data, via system-specific, black-box force fields

Julien Steffen and Bernd Hartke 2017
Highlighted by Jan Jensen

Figure 1 from the paper. A flowchart of the EVB-QMDFF program implemented in this work, for the case of a DG-EVB-QMDFF calculation.

A few years ago I highlighted Grimme's General Quantum Mechanically Derived Force Field (QMDFF) - a black box approach that gives you a system-specific force field from a single QM Hessian calculation.  I missed the fact that Hartke and Grimme extended this approach to TSs using EVB, a year later. This EVB-QMDFF approach constructs EVB potentials connecting each pair of minima described by QMDFF.  To get the EVB parameters you need to supply the TS and 10-100 energies (and possibly 5-10 Hessian calculations) along the reaction path, depending on how complex an EVB potential is needed to describe the reaction.

What's the point of a system-specific reactive force field when you already have the TS and reaction path? Well, Steffen and Hartke show is that EVB-QMDFF can be used to perform the additional calculations needed for, for example, variational TS theory or ring polymer MD calculations to get more accurate rate constants.

Furthermore, just like for QMDFF for minima you could do all this for one conformation of ligands and use EVB-QMDFF for a conformer search or use the gas phase parameterized model to study the effect of explicit solvation.  It might even be possible to parameterize EVB-QMDFF using small ligands and then model the effect of larger ligands using the QMDFF parameters obtained for the minima.  However, all these potential uses still need to be tested.

I thank Jean-Philip Piquemal for bringing this paper to my attention



This work is licensed under a Creative Commons Attribution 4.0 International License.

Ab Initio Calculation of Rate Constants for Molecule–Surface Reactions with Chemical Accuracy

GiovanniMaria Piccini, Maristella Alessio, and Joachim Sauer (2016)

Contributed by Jan Jensen

Piccini et al. reproduce experimental rate constants for the reactions of methanol with ethene, propene, and trans-2-butene catalyzed by an acidic zeolite (H-MFI), to within one order of magnitude. Key to this is the inclusion of anharmonic effects using the method I highlighted earlier, but it should be noted that the reaction is biomolecular so entropy effects may be larger than for unimolecular reactions such as most enzyme catalysed reactions. However, anharmonic effects also changed the activation enthalpy by as much as 8 kJ/mol.

The PBE/plane wave electronic energy is corrected using MP2/CBS computed for a smaller systems plus a CCSD(T)/TZVP correction computed on an even smaller system.  Such corrections are becoming increasingly feasible for many problems and this study shows that the usual harmonic treatment of the vibrational free energy may become the limiting factor in terms of accuracy. However, anharmonic methods such as the one used here must be implemented, in a black box-fashion, in at least one of the major quantum chemistry packages before we'll see them widely applied.

See also this highlight of the article



This work is licensed under a Creative Commons Attribution 4.0

Dehydro-Diels-Alder Reactions

Contributed by Steven Bacharach

Reposted from Computational Organic Chemistry with permission

I have been delinquent in writing about the dehydro-Diels-Alder reactions, but really can’t put it off any further. These sets of reactions really deserve a fuller analysis than I am going to summarize here, but this post will provide a good jumping off point for anyone interested in further investigation.

So the Diels-Alder reaction is among the most famous and most important reactions in organic chemistry. The reaction creates a 6-member ring and sets up to four stereocenters. In the past couple of years many chemists have expressed interest in the variant where the four-carbon component is more highly unsaturated, i.e. enyne or diyne. I will summarize the results of three recent computational papers dealing with the reaction of a diyne with an yne.

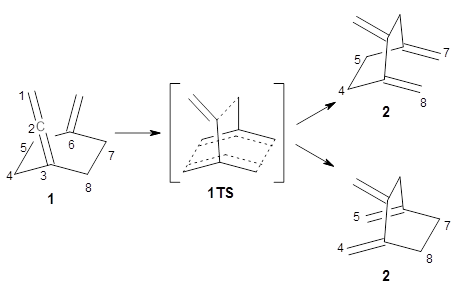
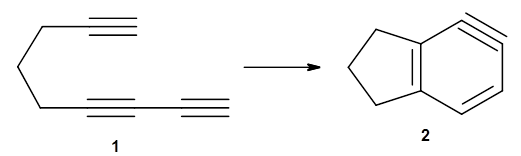
The first paper is by Skraba-Joiner, Johnson, and Agarwal.¹ They discuss, among a number of interesting pericyclic reactions, the intramolecular Diels-Alder reaction of triyne 1 to give 2. They examined a concerted and stepwise pathway at (U)M05-2X/6-311+G(d,p) and find the concerted to be favored by 6.0 kcal mol^-1. CCSD(T) using these geometries increases the difference to 8.2 kcal mol^-1. The T₁ diagnostic is fairly large for both the concerted and stepwise transition states, so they also performed CCSD(T)/CBS computations, which had much lower T₁ values. The concerted TS remained favorable, but by only 2.7 kcal mol^-1.

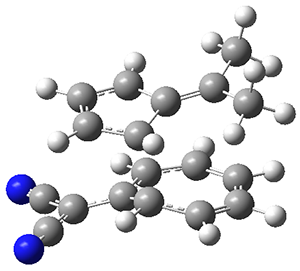
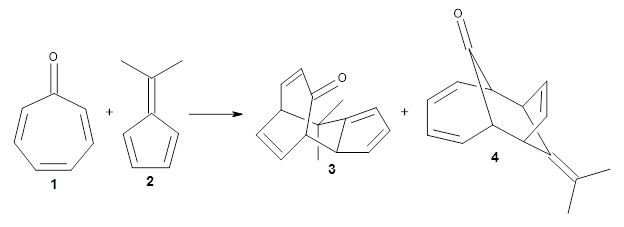
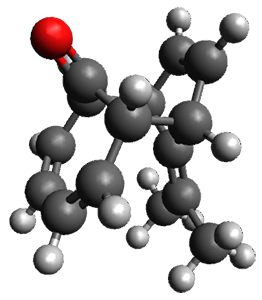
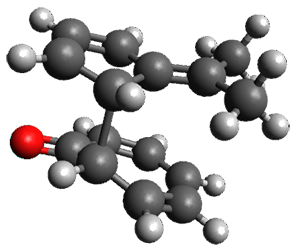
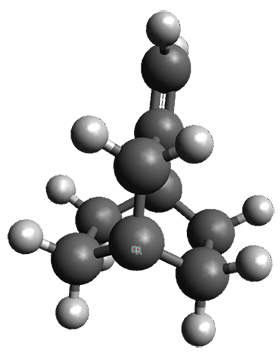
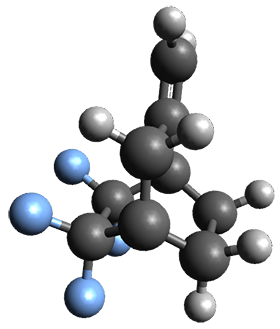
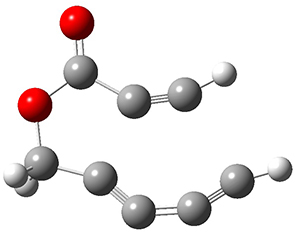
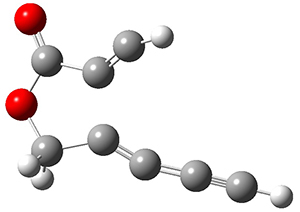
In the same special issue of the Journal of Organic Chemistry, Cramer, Hoye, and Kuwata examined a reaction closely related to what Johnson examined above.² They looked at the reaction taking 3 into 4 via both experiments and computations. The M06-2x/6-311+G(d,p) geometries for the concerted and first TS along the stepwise path (with R1=R2=H) are shown in Figure 1. Evaluating the energies at SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p) find in this case (along with all of the other R1/R2 variants they examined) that the stepwise path has a lower barrier than the concerted path. In the case where R1=R2=H, the stepwise path is favored by 6.0 kcal mol^-1. Additionally, these stepwise barriers are in reasonable agreement with the experimentally-derived barriers.

Concerted TS

Stepwise TS

Figure 1. M06-2x/6-311+G(d,p) optimized geometries of the concerted and stepwise TSs for the reaction of 3H going to 4H.

It should be pointed out that the wavefunctions for the concerted TSs were all found to be unstable with regard to a restricted to unrestricted relaxation. Given this problem, they also performed a CASPT2 energy evaluation of the concerted and stepwise transition states for the case R1=R2=H. CASPT2 finds the stepwise barrier to be 3.7 kcal mol^-1 lower than the concerted barrier.

The last paper comes from the Houk lab, and examines the simplest set of intermolecular dehdro-Diels-Alder reactions.³ I will focus here on the most unsaturated analogue, the reaction of 1,3-butadiyne 5 with ethyne to give benzyne 6.

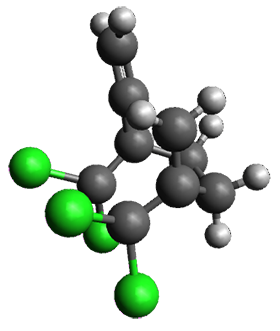
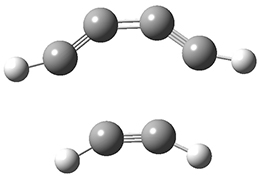
The concreted and stepwise transition states for this reaction (at (U)M06-2X/6-311+G(d,p)) are shown in Figure 2. The concerted barrier is 36.0 kcal moml^-1 while the stepwise barrier is slightly lower: 35.2 kcal mol^-1. The distortion energy for the concerted reaction is large (43.2 kcal mol^-1) due mostly to angle changes in the diyne. Its interaction energy is -7.2 kcal mol^-1, similar to the interaction energy in other similar Diels-Alder reactions. In contrast, the distortion energy for the stepwise pathway is 27.5 kcal mol^-1, but the interaction energy is +7.7 kcal mol^-1. These values are very similar to the distortion and interaction energy of the related (but less saturated DA reactions).

Concerted TS

Stepwise TS

Figure 2. (U)M06-2X/6-311+G(d,p) optimized concerted and stepwise TS for the reaction of 1,3-diyne with ethyne.

Molecular dynamics trajectories for both the concerted and stepwise paths reveal interesting differences. The concerted trajectories show an oscillatory behaviour of bending the angles at the C2 and C3 carbons prior to the TS, and then near synchronous formation of the new C-C bonds. The trajectories initiated at the stepwise TS show no systematic motion. Once the bond is formed, the biradical exhibits a long lifetime, on the order of picoseconds, much longer than the trajectory runs.

These three studies indicate the nature of the dehydro Diels-Alder reaction is very sensitive to reaction conditions, substituents, solvation, and all other manner of effects and will likely prove an area of interest for some time. It should keep a number of computational chemists busy for some time!

References

(1) Skraba-Joiner, S. L.; Johnson, R. P.; Agarwal, J. "Dehydropericyclic Reactions: Symmetry-Controlled Routes to Strained Reactive Intermediates," J. Org. Chem. 2015, 80, 11779-11787, DOI:10.1021/acs.joc.5b01488.

(2) Marell, D. J.; Furan, L. R.; Woods, B. P.; Lei, X.; Bendelsmith, A. J.; Cramer, C. J.; Hoye, T. R.; Kuwata, K. T. "Mechanism of the Intramolecular Hexadehydro-Diels–Alder Reaction," J. Org. Chem. 2015, 80, 11744-11754, DOI: 10.1021/acs.joc.5b01356.

(3) Yu, P.; Yang, Z.; Liang, Y.; Hong, X.; Li, Y.; Houk, K. N. "Distortion-Controlled Reactivity and Molecular Dynamics of Dehydro-Diels–Alder Reactions," J. Am. Chem. Soc. 2016, 138, 8247-8252, DOI:10.1021/jacs.6b04113.

InChIs

1: InChI=1S/C9H8/c1-3-5-7-9-8-6-4-2/h1-2H,5,7,9H2
InChIKey=IYZAZSVBWMMSLQ-UHFFFAOYSA-N

2: InChI=1S/C9H8/c1-2-5-9-7-3-6-8(9)4-1/h1,4H,3,6-7H2
InChIKey=PZJMTUKDGZUDBH-UHFFFAOYSA-N

3H: InChI=1S/C8H4O2/c1-3-5-6-7-10-8(9)4-2/h1-2H,7H2
InChIKey=MGXDIFXPYGGQLF-UHFFFAOYSA-N

4H: InChI=1S/C10H8O4/c1-6(11)14-8-2-3-9-7(4-8)5-13-10(9)12/h2-4H,5H2,1H3
InChIKey=GEFLHLNIKGXWCA-UHFFFAOYSA-N

5: InChI=1S/C4H2/c1-3-4-2/h1-2H
InChIKey=LLCSWKVOHICRDD-UHFFFAOYSA-N

6: InChI=1S/C6H4/c1-2-4-6-5-3-1/h1-4H
InChIKey=KLYCPFXDDDMZNQ-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.