Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model

Bickelhaupt, F. M.; Houk, K. N.,  Angew. Chem. Int. Ed. 2017, 56, 10070-10086
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Bickelhaupt and Houk present a nice review of their separately developed, but conceptually identical model for assessing reactivity.¹ Houk termed this the “distortion/interaction” model,² while Bickelhaupt named it “activation strain”.³ The concept is that the activation barrier can be dissected in a distortion or stain energy associated with bringing the reactants into the geometry of the transition state, and the interaction energy is the stabilization energy afforded by the molecular orbital interactions of the reactant components with each other in the transition state.

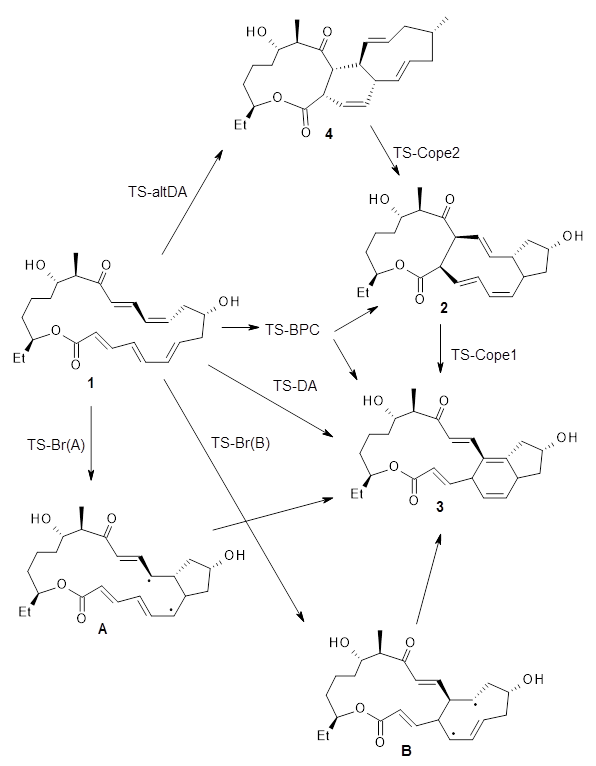
The review discusses a broad range of applications, including S_N2 and E₂ reactions, pericyclic reactions (including Diels-Alder reactions of enones and the dehdydro Diels-Alder reaction that I have discussed in this blog), a click reaction, a few examples involving catalysis, and the regioselectivity of indolyne (see this post). They also discuss the role of solvent and the relationship of this model to Marcus Theory.

I also want to mention in passing a somewhat related article by Jorgensen and co-authors published in the same issue of Angewandte Chemie as the above review.⁴ This article discusses the paucity of 10 electron cycloaddition reactions, especially in comparison to the large number of very important cycloaddition reactions involving 6 electrons, such as the Diels-Alder reaction, the Cope rearrangement, and the Claisen rearrangement. While the article does not focus on computational methods, computations have been widely used to discuss 10-electron cycloadditions. The real tie between this paper and the review discussed above is Ken Houk, whose graduate career started with an attempt to perform a [6+4] cycloaddition, and he has revisited the topic multiple times throughout his career.

References

1. Bickelhaupt, F. M.; Houk, K. N., "Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model." Angew. Chem. Int. Ed. 2017, 56, 10070-10086, DOI: 10.1002/anie.201701486.

2. Ess, D. H.; Houk, K. N., "Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity." J. Am. Chem. Soc. 2007, 129, 10646-10647, DOI: 10.1021/ja0734086

3. Bickelhaupt, F. M., "Understanding reactivity with Kohn-Sham molecular orbital theory: E2-S_N2 mechanistic spectrum and other concepts." J. Comput. Chem. 1999, 20, 114-128

4. Palazzo, T. A.; Mose, R.; Jørgensen, K. A., "Cycloaddition Reactions: Why Is It So
Challenging To Move from Six to Ten Electrons?" Angew. Chem. Int. Ed. 2017, 56, 10033-10038, DOI: 10.1002/anie.201701085.

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Quantifying Possible Routes for SpnF-Catalyzed Formal Diels–Alder Cycloaddition

Medvedev, M. G.; Zeifman, A. A.; Novikov, F. N.; Bushmarinov, I. S.; Stroganov, O. V.; Titov, I. Y.; Chilov, G. G.; Svitanko, I. V., J. Am. Chem. Soc. 2017, 139, 3942-3945
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Medvedev, et al. have examined the cyclization step in the formation of Spinosyn A, which is catalyzed by the putative Diels-Alderase enzyme SpnF.¹ This work follows on the computational study done by Houk, Singleton and co-workers,² which I have discussed in this post (Dynamics in a reaction where a [6+4] and [4+2] cycloadditons compete). In fact, I recommend that you read the previous post before continuing on with this one. In summary, Houk, et al. found that a single transition state connects reactant 1 to both 2 and 3. The experimental product with the enzyme SpnF is 3. In the absence of enzyme, Houk, et al. suggest that reactions will cross the bispericyclic transition state TS-BPC (TS1 in the previous post) leading primarily to 2, which then undergoes a Cope rearrangement to get to product 3. Some molecules will follow pathways that go directly to 3.

The PCM(water)/M06-2x/6-31+G(d) study by Medvedev, et al. first identifies 560 conformations of 3. Next, they identified 384 TSs lying within 30 kcal mol^-1 from the lowest TS. These can be classified as either TS-DA (leading directly to 3) or TS-BPC (which may lead to 2 by steepest descent, but can bifurcate towards 3). They opt to utilize the Atoms-in-Molecules theory to identify bond critical points to categorize these TS, and find that 144 are TS-BPC and 240 are TS-DA. (The transition state found by Houk, et al. is the second lowest energy TS found in this study, 0.29 kcal mol^-1 higher in energy that the lowest TS and also of TS-BPC type.)

They also examined two alternative routes. First, they propose a path that first takes 1 to 4 via an alternative Diels-Alder reaction, and a second Cope rearrangement (TS-Cope2) takes this to 2, which can then convert to 3 via TS-Cope1. The other route involves a biradical pathway to either A or B. These alternatives prove to be non-competitive, with transition state energies significantly higher than either TS-DA or TS-BPC.

Returning to the set of TS-DA and TS-BPC transition states, while the former are more numerous, the latter are lower in energy. In summary, this study further complicates the complex situation presented by Houk, et. al. In the absence of catalyst, 1 can undergo either a Diels-Alder reaction to 3, or pass through a bispericyclic transition state that can lead to 3, but principally to 2 and then undergo a Cope rearrangement to get to 3. The question that ends my previous post on this subject — “ just what role does the enzyme SpnF play?” — remains to be answered.

References

1) Medvedev, M. G.; Zeifman, A. A.; Novikov, F. N.; Bushmarinov, I. S.; Stroganov, O. V.; Titov, I. Y.; Chilov, G. G.; Svitanko, I. V., "Quantifying Possible Routes for SpnF-Catalyzed Formal Diels–Alder Cycloaddition." J. Am. Chem. Soc. 2017, 139, 3942-3945, DOI: 10.1021/jacs.6b13243.

2) Patel, A.; Chen, Z.; Yang, Z.; Gutiérrez, O.; Liu, H.-w.; Houk, K. N.; Singleton, D. A., "Dynamically Complex [6+4] and [4+2] Cycloadditions in the Biosynthesis of Spinosyn A." J. Am. Chem. Soc. 2016, 138, 3631-3634, DOI: 10.1021/jacs.6b00017.

InChIs

1: InChI=1S/C24H34O5/c1-3-21-15-12-17-23(27)19(2)22(26)16-10-7-9-14-20(25)13-8-5-4-6-11-18-24(28)29-21/h4-11,16,18-21,23,25,27H,3,12-15,17H2,1-2H3/b6-4+,8-5+,9-7+,16-10+,18-11+/t19-,20+,21-,23-/m0/s1
InChIKey=JEKALMRMHDPSQK-ZTRRSECRSA-N

2: InChI=1S/C24H34O5/c1-3-19-8-6-10-22(26)15(2)23(27)20-12-11-17-14-18(25)13-16(17)7-4-5-9-21(20)24(28)29-19/h4-5,7,9,11-12,15-22,25-26H,3,6,8,10,13-14H2,1-2H3/b7-4-,9-5+,12-11+/t15-,16-,17-,18-,19+,20+,21-,22+/m1/s1
InChIKey=AVLPWIGYFVTVTB-PTACFXJJSA-N

3: InChI=1S/C24H34O5/c1-3-19-5-4-6-22(26)15(2)23(27)11-10-20-16(9-12-24(28)29-19)7-8-17-13-18(25)14-21(17)20/h7-12,15-22,25-26H,3-6,13-14H2,1-2H3/b11-10+,12-9+/t15-,16+,17-,18-,19+,20-,21-,22+/m1/s1
InChIKey=BINMOURRBYQUKD-MBPIVLONSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Simulation-Based Algorithm for Two-Dimensional Chemical Structure Diagram Generation of Complex Molecules and Ligand–Protein Interactions

Frączek, T. J. Chem. Inform. Model. 2016, 56, 2320-2335
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Making a good drawing of a chemical structure can be a difficult task. One wants to prepare a drawing that provides a variety of different information in a clean and clear way. We tend to want equal bond lengths, angles that are representative of the atom’s hybridization, symmetrical rings, avoided bond crossings, and the absence of overlapping groups. These ideals may be difficult to manage. Sometimes we might also want to represent something about the actual 3-dimensional shape. So for example, the drawing on the left of Figure 1 properly represents the atom connectivity with no bond crossing, but the figure on the right is probably the image all organic chemists would want to see for cubans.

Figure 1. Two drawing of cubane

For another example, the drawing on the left of Figure 2 nicely captures the relative stereo relationships within D-glucose, but the drawing on the right adds in the fact that the cyclohexyl ring is in a chair conformation. Which drawing is better? Well, it likely is in the eye of the beholder, and the context of the chemistry at hand.

Figure 2. Two drawings of D-glucose.

Frączek has reported on an automated procedure for creating aesthetically pleasing 2-D drawings of chemical structures.¹ The method involves optimizing distances between atoms projected onto a 2-D plane, along with rules to try to keep atom lengths and angles similar, and symmetrical rings, and minimize overlapping bonds. He shows a number of nice examples, especially of natural products, where his automated procedure PSM (physical simulation method) provides some very nice drawings, often noticeably superior to those generated by previously proposed schemes for preparing drawings.

Using the web site he has developed (http://omnidepict.p.lodz.pl/), I recreated the structures of some of the molecules I have discussed in this blog. In Figure 3, these are shown side-by-side to my drawings. My drawings were generally done with MDL/Isis/Accelrys/Biovia Draw (available for free for academic users) with an eye towards representing what I think is a suitable view of the molecule based on what I am discussing in the blog post. For many molecules, PSM does a very nice job, sometimes better than what I have drawn, but in some cases PSM produces an inferior drawing. Nonetheless, creating nice chemical drawings can be tedious and PSM offers a rapid option, worthy of at least trying out. Ultimately, what we decide to draw and publish is often an aesthetic choice and each individual must decide on one’s own how best to present one’s work.

My Drawing	PSM

Figure 3. Comparison of my drawings vs. drawing made by PSM.

References

1) Frączek, T., "Simulation-Based Algorithm for Two-Dimensional Chemical Structure Diagram Generation of Complex Molecules and Ligand–Protein Interactions." J. Chem. Inform. Model. 2016, 56, 2320-2335, DOI: 10.1021/acs.jcim.6b00391.

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Polytriangulane

Allen, W. D.; Quanz, H.; Schreiner, P. R. J. Chem. Theory Comput. 2016, 12, 4707–4716

Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Cyclopropyl rings can be joined together in a spiro fashion to form triangulanes. An interesting topology can be made by joining the rings to form a helical pattern, as shown in the [9]triangulane 1 below. Allen, Quanz, and Schreiner¹ have examined the notion of an infinite helical molecule formed in this way.

1

First, they describe how one can generate the coordinates of such a beast using a closed analytical expression, which is a really nice demonstration of applied geometry. Next, they compute the geometry of a series of [n]triangulanes at M06-2x/6-31G(d). The geometries of [9]triangulane and their largest example, [42]triangulane 2 are shown in Figure 1.

1

2

Figure 1. M06-2x/6-31G(d) optimized geometries of 1 and 2.

They show that the geometry of 2 exhibits a structure that has two different C-C distances: one between the spiro carbons, and the second between the spiro carbon and the methylene carbon. The distance between the spiro carbons is rather short (1.458 Å), suggesting that the bonding here is between carbons that are nearly sp²-hybridized.

Lastly, they discuss the thermodynamics of polytriangulane. They employ a series of homodesmotic reactions to attempt to determine the enthalpy for adding another cyclopropyl ring to an extended triangulane. Unfortunately, the computed enthalpy is quite dependent on functional used. Similar attempts to define the strain energy is also flawed in this way. However, regardless of the functional the enthalpy for adding a cyclopropane ring appears to reach an asymptote rather quickly. So, using [3]triangulane they estimate that the strain energy per mole of cyclopropane in triangulane is about 42.7 kcal mol^-1, or about 14 kcal mol^-1 of strain due to the spiroannulation.

References

(1) Allen, W. D.; Quanz, H.; Schreiner, P. R. “Polytriangulane,” J. Chem. Theory Comput. 2016, 12, 4707–4716, DOI: 10.1021/acs.jctc.6b00669.

InChIs

1: InChI=1S/C19H22/c1-2-12(1)5-14(12)7-16(14)9-18(16)11-19(18)10-17(19)8-15(17)6-13(15)3-4-13/h1-11H2/t14-,15-,16-,17-,18-,19-/m0/s1
InChIKey=XBTZCZDSKVTALB-DYKIIFRCSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Redox-Dependent Transformation of a Hydrazinobuckybowl between Curved and Planar Geometries

Higashibayashi, S.; Pandit, P.; Haruki, R.; Adachi, S.-I.; Kumai, R. Angew. Chem. Int. Ed. 2016, 55, 10830-10834
Contributed by Steven Bacharach
Reposted from Computational Organic Chemistry with permission

Higashibayashi and co-workers prepared the hydrazine-substituted Buckyball fragment 1a and also its mono- and deoxidized analogues.¹ To interpret their results, they also computed the parent structure 1bat ωB97Xd/6-311+G(d,p).

1a R = tBut 1b R = H

The optimized structure of 1b is a bowl, but a twisted geometry, where the lone pair on each
nitrogen is on the opposite face of the molecule, lies only 1.6 kcal mol^-1 higher in energy. The barrier for moving from the bowl to the twist form is 2.0 kcal mol^-1. The completely planar structure, which is also a transition state for inversion of the bowl, lies 5.1 kcal mol^-1 above the lowest energy bowl structure. The geometries and energies of the conformations are shown in Figure 1.

1b bowl (0.0)	1b twist (1.6)
1b TS (2.0)	1b planar TS (5.11)

Figure 1. ωB97Xd/6-311+G(d,p) optimized
geometry and relative energy (kcal mol^-1) of the conformations of 1b.

The mono oxidized 1b^.+ structure is also a bowl, but there is no twist form and inversion takes place through a planar structure that is only 0.5 kcal mol^-1 above the bowl ground state. The structures and energies of these conformations of 1b^.+ are shown in Figure 2.

1b.+ bowl (0.0)

1b.+ planar TS (0.5)

Figure 2. ωB97Xd/6-311+G(d,p) optimized geometry and relative energy (kcal mol^-1) of the conformations of 1b^.+.

Lastly, the di-oxidized 1b²⁺ is planar, and its structure is shown in Figure 3.

1b2+ planar

Figure 2. ωB97Xd/6-311+G(d,p) optimized geometry of 1b²⁺.

These computations corroborate all of the experimental data observed with 1a. What is particularly of note is the fact that the potential energy surface is so dependent on charge state: a three-well potential for the neutral, and two-well potential for the monocation, and a single-well potential for the dication.

References

(1) Higashibayashi, S.; Pandit, P.; Haruki, R.; Adachi, S.-I.; Kumai, R. “Redox-Dependent
Transformation of a Hydrazinobuckybowl between Curved and Planar Geometries,” Angew. Chem. Int. Ed.2016, 55, 10830-10834, DOI: 10.1002/anie.201605340.

InChIs

1a: InChI=1S/C40H44N2/c1-37(2,3)21-13-25-26-14-22(38(4,5)6)19-31-32-20-24(40(10,11)12)16-28-27-15-23(39(7,8)9)18-30-29(17-21)33(25)41(34(26)31)42(35(27)30)36(28)32/h13-20H,1-12H3
InChIKey=DKJNIDLSMMQIBX-UHFFFAOYSA-N

1b:InChI=1S/C24H12N2/c1-5-13-14-6-2-11-19-20-12-4-8-16-15-7-3-10-18-17(9-1)21(13)25(22(14)19)26(23(15)18)24(16)20/h1-12H
InChIKey=JQNPHLTXAOKXNQ-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Reactivity and Selectivity of Bowl-Shaped Polycyclic Aromatic Hydrocarbons: Relationship to C60

García-Rodeja, Y.; Solà, M.; Bickelhaupt , F. M.; Fernández, I. Chem. Eur. J. 2016, 22, 1368-1378
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Fullerenes can undergo the Diels-Alder reaction with some specificity: the diene preferentially adds across the bond shared by two fused 6-member rings over the bond shared by the fused 6- and 5-member rings. Garcia-Rodeja and colleagues have examined the analogous Diels-Alder reaction of cyclopentadiene with five curved aromatic compounds, 1-5.¹

The computations were performed at BP86-D3/def2-TZVPP//RI-BP86-D3/def2-SVP. Representative transition states for the addition of cyclopentadiene with 3 over the 6,6-bond and 5,6-bond are shown in Figure 1.

5,6-bond

6,6-bond

Figure 1. RI-BP86-D3/def2-SVP optimized transition states for the reaction of cyclopentadiene with 3.

For the reactions of cyclopentadiene with 2-5 the reactions with the 6,6-bond is both kinetically and thermodynamically favored, while with 1 the 6,6-bond is kinetically preffered and the 5,6-adduct is the thermodynamic product. As the molecules increase in size (from 1 to 5), the activation barrier decreases, and the barrier for the reaction with 5 is only 1.4 kcal mol^-1larger than the barrier with C₆₀. The reaction energy also becomes more exothermic with increasing size. There is a very good linear relationship between activation barrier and reaction energy.

Use of the distortion/interaction model indicates that the preference for the 6,6-regioselectivity come from better interaction energy than for the 5,6-reaction, and this seems to come about by better orbital overlap between the cyclopentadiene HOMO and the 6,6-LUMO of the buckybowl.

References

(1) García-Rodeja, Y.; Solà, M.; Bickelhaupt , F. M.; Fernández, I. "Reactivity and Selectivity of Bowl-Shaped Polycyclic Aromatic Hydrocarbons: Relationship to C60," Chem. Eur. J. 2016, 22, 1368-1378, DOI:<10.1002/chem.201502248.

InChIs

1: InChI=1S/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey=VXRUJZQPKRBJKH-UHFFFAOYSA-N

2: InChIKey=ASIFYFRJNYNQLA-UHFFFAOYSA-N

3: InChI=1S/C26H12/c1-5-13-14-6-2-11-19-20-12-4-8-16-15-7-3-10-18-17(9-1)21(13)25(22(14)19)26(23(15)18)24(16)20/h1-12H
InChIKey=OUWFOTSXASFGQD-UHFFFAOYSA-N

4: InChI=1S/C30H12/c1-2-14-6-10-18-20-12-8-16-4-3-15-7-11-19-17-9-5-13(1)21-22(14)26(18)29(25(17)21)30-27(19)23(15)24(16)28(20)30/h1-12H
InChIKey=JEUCRZPADDQRKU-UHFFFAOYSA-N

5: InChI=1S/C36H12/c1-7-16-17-9-3-14-5-11-20-21-12-6-15-4-10-19-18-8-2-13(1)22-25(16)31-32(26(18)22)34-28(19)24(15)30(21)36(34)35-29(20)23(14)27(17)33(31)35/h1-12H
InChIKey=QMGQDOOJOCPYIA-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Benchmarking Continuum Solvent Models for Keto–Enol Tautomerizations

McCann, B. W.; McFarland, S.; Acevedo, O. J. Phys. Chem. A 2015, 119, 8724-8733
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

The keto-enol tautomerization is a fundamental concept in organic chemistry, taught in the introductory college course. As such, it provides an excellent test reaction to benchmark the performance computational methods. Acevedo and colleagues have reported just such a benchmark study.¹

First, the compare a wide variety of methods, ranging from semi-empirical, to DFT, and to composite procedures, with experimental gas-phase free energy of tautomerization. They use seven such examples, two of which are shown in Scheme 1. The best results from each computation category are AM1, with a mean absolute error (MAE) of 1.73 kcal mol^-1, M06/6-31+G(d,p), with a MAE of 0.71 kcal mol^-1, and G4, with a MAE of 0.95 kcal mol^-1. All of the modern functionals do a fairly good job, with MAEs less than 1.3 kcal mol^-1.

Scheme 1

As might be expected, the errors were appreciably larger for predicting the free energy of tautomerization, with a good spread of errors depending on the method for handling solvent (PCM, CPCM, SMD) and the choice of cavity radius. The best results were with the G4/PCM/UA0 procedure, though M06/6-31+G(d,p)/PCM and either UA0 or UFF performed quite well, at considerably less computational expense.

References

(1) McCann, B. W.; McFarland, S.; Acevedo, O. "Benchmarking Continuum Solvent Models for Keto–Enol Tautomerizations," J. Phys. Chem. A 2015, 119, 8724-8733, DOI: 10.1021/acs.jpca.5b04116.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.