Daria E. Kim, Joshua E. Zweig and Timothy R. Newhouse (2018)
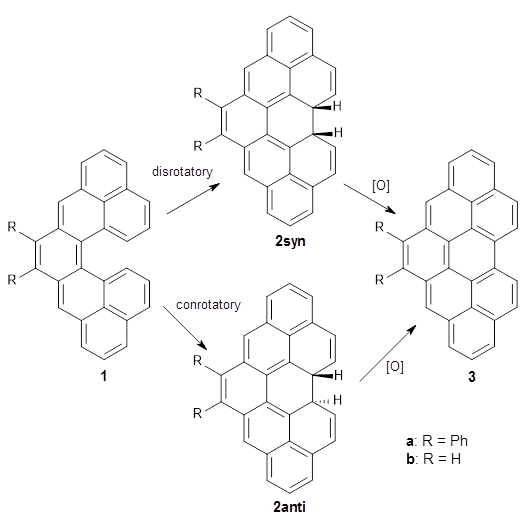
This paper presents a rare example of using quantum chemical TS calculations to guide, rather than post-rationalise, organic synthesis. The authors wanted to design a retrosynthetic path that could be used to make two related natural products, paspaline A and emindole PB, that require either a ring closure (paspaline A) or a methyl shift (emindole PB). Three different routes were possible that lead to different functionalities that were relatively distant from the ring closure/methyl shift, which made it hard to predict the best route by chemical intuition.
Instead the authors used mPW1PW91/6-31+G(d,p)//B3LYP/6-31G(d) to find the TSs for both reactions for each of the three routes to predict the best route, which turns out to be "C". Route C did indeed work great in practice, while route A (predicted to be worst route) didn't give the desired results.
My guess is that the key here is that the synthetic question was reduced to a question of relative barrier heights of closely related reactions, i.e. ΔΔΔG‡ = ΔΔG‡(4→5) - ΔΔG‡(4→6), which leads to maximum error cancellation. I hope this paper will lead to more use of QM to guide synthetic decisions and more work on making TS calculations even more accessible to synthetic chemists

This work is licensed under a Creative Commons Attribution 4.0 International License.
Highlighted by Jan Jensen
Figure 2 from the paper reproduced under the CC-BY-NC-ND licence
This paper presents a rare example of using quantum chemical TS calculations to guide, rather than post-rationalise, organic synthesis. The authors wanted to design a retrosynthetic path that could be used to make two related natural products, paspaline A and emindole PB, that require either a ring closure (paspaline A) or a methyl shift (emindole PB). Three different routes were possible that lead to different functionalities that were relatively distant from the ring closure/methyl shift, which made it hard to predict the best route by chemical intuition.
Instead the authors used mPW1PW91/6-31+G(d,p)//B3LYP/6-31G(d) to find the TSs for both reactions for each of the three routes to predict the best route, which turns out to be "C". Route C did indeed work great in practice, while route A (predicted to be worst route) didn't give the desired results.
My guess is that the key here is that the synthetic question was reduced to a question of relative barrier heights of closely related reactions, i.e. ΔΔΔG‡ = ΔΔG‡(4→5) - ΔΔG‡(4→6), which leads to maximum error cancellation. I hope this paper will lead to more use of QM to guide synthetic decisions and more work on making TS calculations even more accessible to synthetic chemists

This work is licensed under a Creative Commons Attribution 4.0 International License.