Navigating molecular space for reaction mechanisms: an efficient, automated procedure

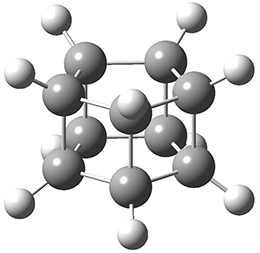
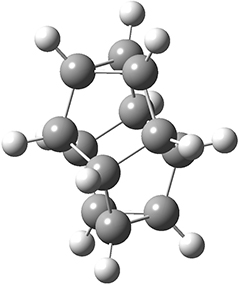
Paul M. Zimmerman (2015)
Contributed by Jan Jensen

This methodology takes a single structure as input automatically finds related intermediates and transition states connecting them to map out entire reaction mechanisms.  The methodology is the combination of two different methods.

A single elementary step search "that takes a single chemical structure and proposes new intermediates that could be one elementary step away". Here an "elementary step" is defined as "chemical rearrangements with no more than two connections breaking and two connections forming simultaneously, while maintaining the upper and lower limits for coordination number of each atom." The energy of these intermediates are then computed using DFT and the ones with sufficiently low energy are kept.

The Growing String Method is then used to find the transition state and reaction path connecting the intermediates to the input structure and reaction paths with sufficiently low barriers are kept.  This method, as implemented in Q-Chem, is completely automated and appears to be very robust.

The procedure is then repeated using the remaining intermediates as input until no new intermediates are formed.  The thermodynamic and kinetic screening helps insure that the number of intermediates do no grow out of control.  Also, for larger systems one can define inactive atoms (e.g. non-reactive ligands) that are not considered when creating new intermediates.


This work is licensed under a Creative Commons Attribution 4.0

Reactivity and Selectivity of Bowl-Shaped Polycyclic Aromatic Hydrocarbons: Relationship to C60

García-Rodeja, Y.; Solà, M.; Bickelhaupt , F. M.; Fernández, I. Chem. Eur. J. 2016, 22, 1368-1378
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Fullerenes can undergo the Diels-Alder reaction with some specificity: the diene preferentially adds across the bond shared by two fused 6-member rings over the bond shared by the fused 6- and 5-member rings. Garcia-Rodeja and colleagues have examined the analogous Diels-Alder reaction of cyclopentadiene with five curved aromatic compounds, 1-5.¹

The computations were performed at BP86-D3/def2-TZVPP//RI-BP86-D3/def2-SVP. Representative transition states for the addition of cyclopentadiene with 3 over the 6,6-bond and 5,6-bond are shown in Figure 1.

5,6-bond

6,6-bond

Figure 1. RI-BP86-D3/def2-SVP optimized transition states for the reaction of cyclopentadiene with 3.

For the reactions of cyclopentadiene with 2-5 the reactions with the 6,6-bond is both kinetically and thermodynamically favored, while with 1 the 6,6-bond is kinetically preffered and the 5,6-adduct is the thermodynamic product. As the molecules increase in size (from 1 to 5), the activation barrier decreases, and the barrier for the reaction with 5 is only 1.4 kcal mol^-1larger than the barrier with C₆₀. The reaction energy also becomes more exothermic with increasing size. There is a very good linear relationship between activation barrier and reaction energy.

Use of the distortion/interaction model indicates that the preference for the 6,6-regioselectivity come from better interaction energy than for the 5,6-reaction, and this seems to come about by better orbital overlap between the cyclopentadiene HOMO and the 6,6-LUMO of the buckybowl.

References

(1) García-Rodeja, Y.; Solà, M.; Bickelhaupt , F. M.; Fernández, I. "Reactivity and Selectivity of Bowl-Shaped Polycyclic Aromatic Hydrocarbons: Relationship to C60," Chem. Eur. J. 2016, 22, 1368-1378, DOI:<10.1002/chem.201502248.

InChIs

1: InChI=1S/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey=VXRUJZQPKRBJKH-UHFFFAOYSA-N

2: InChIKey=ASIFYFRJNYNQLA-UHFFFAOYSA-N

3: InChI=1S/C26H12/c1-5-13-14-6-2-11-19-20-12-4-8-16-15-7-3-10-18-17(9-1)21(13)25(22(14)19)26(23(15)18)24(16)20/h1-12H
InChIKey=OUWFOTSXASFGQD-UHFFFAOYSA-N

4: InChI=1S/C30H12/c1-2-14-6-10-18-20-12-8-16-4-3-15-7-11-19-17-9-5-13(1)21-22(14)26(18)29(25(17)21)30-27(19)23(15)24(16)28(20)30/h1-12H
InChIKey=JEUCRZPADDQRKU-UHFFFAOYSA-N

5: InChI=1S/C36H12/c1-7-16-17-9-3-14-5-11-20-21-12-6-15-4-10-19-18-8-2-13(1)22-25(16)31-32(26(18)22)34-28(19)24(15)30(21)36(34)35-29(20)23(14)27(17)33(31)35/h1-12H
InChIKey=QMGQDOOJOCPYIA-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Heats of formation of platonic hydrocarbon cages by means of high-level thermochemical procedures

Karton, A.; Schreiner, P. R.; Martin, J. M. L.  J. Comput. Chem. 2016, 37, 49-58
Reposted from Computational Organic Chemistry with permission

Karton, Schreiner, and Martin have benchmarked the heats of formation of some Platonic Solids and related hydrocarbons.¹ The molecules examined are tetrahedrane 1, cubane 2, dodecahedrane 3, trisprismane 4, pentaprismane 5, and octahedrane 6.

The optimized structures (B3LYP-D3BJ/def2-TZVPP) of these compounds are shown in Figure 1.

1	2
3	4
5	6

Figure 1. B3LYP-D3BJ/def2-TZVPP optimized geometries of 1-6.

Using the W1-F12 and W2-F12 composite methods, the estimated the heats of formation of these hydrocarbons are listed in Table 1. Experimental values are available only for 2 and 3; the computed values are off by about 2 kcal mol^-1, which the authors argue is just outside the error bars of the computations. They suggest that the experiments might need to be revisited.

Table 1. Heats of formation (kcal mol^-1) of 1-6.

compound	ΔHf (comp)	ΔHf (expt)
1	128.57
2	144.78	142.7 ± 1.2
3	20.18	22.4 ± 1
4	132.84
5	119.42
6	63.08

They conclude with a comparison of strain energies computed using isogyric, isodesmic, and homodesmotic reactions with a variety of computational methods. Somewhat disappointingly, most DFT methods have appreciable errors compared with the W1-F12 results, and the errors vary depend on the chemical reaction employed. However, the double hybrid method DSD-PBEP86-D3BJ consistently reproduces the W1-F12 results.

References

(1)  Karton, A.; Schreiner, P. R.; Martin, J. M. L. "Heats of formation of platonic hydrocarbon cages by means of high-level thermochemical procedures," J. Comput. Chem. 2016, 37, 49-58, DOI:10.1002/jcc.23963.

InChIs

1: InChI=1S/C4H4/c1-2-3(1)4(1)2/h1-4H
InChIKey=FJGIHZCEZAZPSP-UHFFFAOYSA-N

2: InChI=1S/C8H8/c1-2-5-3(1)7-4(1)6(2)8(5)7/h1-8H
InChIKey=TXWRERCHRDBNLG-UHFFFAOYSA-N

3: InChI=1S/C20H20/c1-2-5-7-3(1)9-10-4(1)8-6(2)12-11(5)17-13(7)15(9)19-16(10)14(8)18(12)20(17)19/h1-20H
InChIKey=OOHPORRAEMMMCX-UHFFFAOYSA-N

4: InChI=1S/C6H6/c1-2-3(1)6-4(1)5(2)6/h1-6H
InChIKey=RCJOMOPNGOSMJU-UHFFFAOYSA-N

5: InChI=1S/C10H10/c1-2-5-3(1)7-8-4(1)6(2)10(8)9(5)7/h1-10H
InChIKey=TXSUZIHPJIZTJT-UHFFFAOYSA-N

6: InChI=1S/C12H12/c1-2-4-6-5(11-7(1)10(4)11)3(1)9-8(2)12(6)9/h1-12H
InChIKey=DUDCBTWUEJEMGD-UHFFFAOYSA-N

'
This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Chromophore−Protein Coupling beyond Nonpolarizable Models: Understanding Absorption in Green Fluorescent Protein

Csaba Daday, Carles Curutchet, Adalgisa Sinicropi, Benedetta Mennucci, and Claudia Filippi, 
J. Chem. Theory Comput. 2015, 11, 4825 – 4839
Contributed by Tobias Schwabe

Modeling enzymichromism, the sprectral tuning of a chromophore by its protein surroundings, is a formidable challenge for computational chemists. It involves methods from molecular dynamics simulations to excited state multi-reference computations in a QM/MM framework (or even more advanced embedding schemes).

Obviously, in each step of the modeling one has to choose from several methods and different applications. As a consequence, no standard protocol how to address the problem has been agreed upon so far. Daday et al. now presented a thorough analysis of possible routes and identified key ingredients for success in enzymichromism modeling in the paper highlighted here. As a test case, they picked the green fluorescent protein (GFP) and the electronic excitation of its chromophore in the protonated (A) and deprotonated (B) form. Two main issues are covered: What is the effect of using an optimized protein structure vs. snapshots from a MD run (and average) and how should the protein environment be modeled?

Let's look at the MD results first: For an average of 50 snapshots, the excitation energies are 3.36 ± 0.1 eV (A form) and 3.07 ± 0.1 eV (B form) at the CAM-B3LYP/6-31+G*/MM level of theory, but the energy spread is 0.5 eV in both cases. Nevertheless, the average is close to the value of an annealed structure (representative for an optimized crystal structure), which the authors also computed: 3.38 eV (A form), 3.11 eV (B form). It is hard to tell if this finding might be transferable to other protein systems or if this good agreement between ensemble average and optimized structure is just a lucky match. The energy spread might be a caveat.

In any case, the obtained values are blue-shifted in comparison to experiment which is not a failure of CAM-B3LYP (alone). This has been checked by recalculating the results with CASPT2/MM. Therefore, the authors also tried different embedding schemes instead of static point charges: state-specific induced dipoles, linear response methods including induced dipoles, and even frozen density embedding (Those readers who want to learn more about the methods and their differences, should refer to [1]). The bottom line: frozen density embedding is not a significant improvement over state-specific induced dipoles, but combining the latter with the effects of linear response in a polarizable embedding yields very good results in comparison. This is in accordance with our previous study of the problem for which CC2 in a polarizable embedding (PERI-CC2) has been applied.[2] There, a very good agreement between PERI-CC2 and all-QM computations has been demonstrated (for smaller cluster models, of course).

The study highlighted here emphasizes the importance of coupling induced dipoles to the transition moments of the excitation which is not done in all methods which allow for polarization in the classical region of a QM/MM approach. These findings also concern the even broader field of solvation models like PCM or COSMO. Everyone interested in environmental effects on electronic excitations (and other dynamical properties) should make oneself familiar with the differences of state-specific and linear response treated polarization effects. Often, they are not pointed out clearly in the literature which hampers a good interpretation of computed results and their assessment in comparison to experiment.


[1] A. S. P. Gomes, C. R. Jacob, Quantum-chemical embedding methods for treating local electronic excitations in complex chemical systems, Annu. Rep. Prog. Chem.,Scet. C:Phys. Chem. 2012, 108, 222–277 (http://dx.doi.org/10.1039/c2pc90007f)
[2] T. Schwabe, M. T. P. Beerepoot, M. T. P., J. M. H. Olsen, J. Kongsted, Analysis of computational models for an accurate study of electronic excitations in GFP Phys. Chem. Chem. Phys. 2015, 17, 2582–2588. (http://dx.doi.org/10.1039/C4CP04524F)