Stefan Grimme and Christoph Bannwarth (2016)
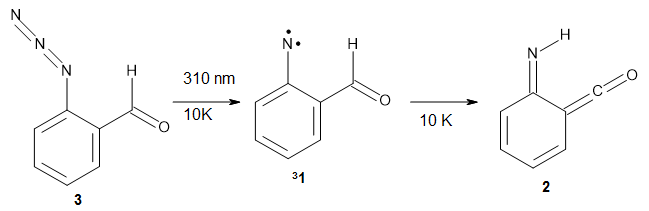
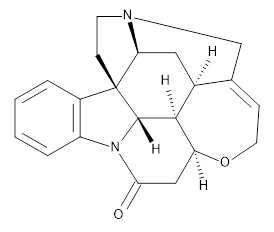
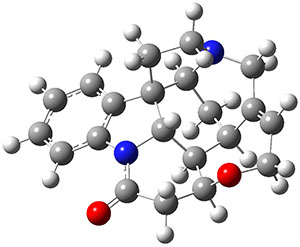
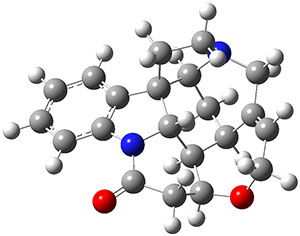
Grimme and Bannwarth presents the xTB method, a modified DFTB2 (SCC-DFTB) method combined with Grimme's simplified Tamm-Dancoff approximated (sTDA) TD-DFT procedure for the rapid calculations of electronic spectra. The two main modifications are 1) the addition of diffuse basis functions for some elements to accurately describe Rydberg states and 2) the SCF is replaced by a single diagonalization and the atomic-charge dependent term is evaluated only once using specifically designed charges. The method is parameterized against CC and DFT calculations for all elements up to Zn and more elements are in the works.
SCS-CC2/aug-cc-VXZ (X = T or D depending on molecule size) vertical singlet-singlet excitation energies are reproduced with a MAE of 0.27 eV. For comparison, the corresponding MAEs for TD-PBE/def2-TZVP and TD-PBE0/def2-SV(P) are 0.67 and 0.31 eV. The method also yields reasonably accurate ECD spectra.
Contributed by Jan Jensen
Grimme and Bannwarth presents the xTB method, a modified DFTB2 (SCC-DFTB) method combined with Grimme's simplified Tamm-Dancoff approximated (sTDA) TD-DFT procedure for the rapid calculations of electronic spectra. The two main modifications are 1) the addition of diffuse basis functions for some elements to accurately describe Rydberg states and 2) the SCF is replaced by a single diagonalization and the atomic-charge dependent term is evaluated only once using specifically designed charges. The method is parameterized against CC and DFT calculations for all elements up to Zn and more elements are in the works.
SCS-CC2/aug-cc-VXZ (X = T or D depending on molecule size) vertical singlet-singlet excitation energies are reproduced with a MAE of 0.27 eV. For comparison, the corresponding MAEs for TD-PBE/def2-TZVP and TD-PBE0/def2-SV(P) are 0.67 and 0.31 eV. The method also yields reasonably accurate ECD spectra.
The method is quite fast requiring only a few minutes of CPU time for molecules with 500-1000 atoms. A very recent paper uses an as-yet-unpublished variant called GFN-xTB to perform an single point calculation on a P450 enzyme (7,500 atoms) without recourse to fragmentation.

This work is licensed under a Creative Commons Attribution 4.0

This work is licensed under a Creative Commons Attribution 4.0