Enhancing NMR Prediction for Organic Compounds Using Molecular Dynamics

Eugene E. Kwan and Richard Y. Liu (2015) DOI 10.1021/acs.jctc.5b00856

Contributed by Jan Jensen

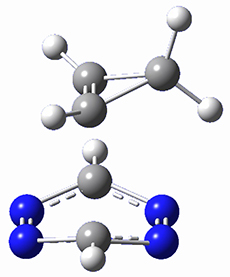
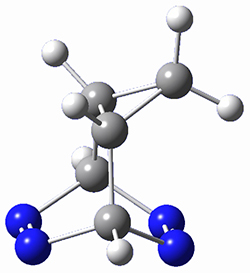
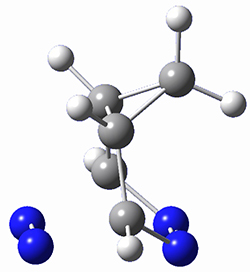
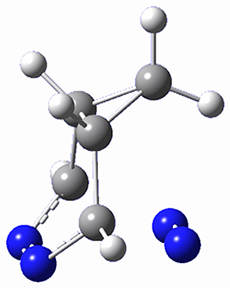
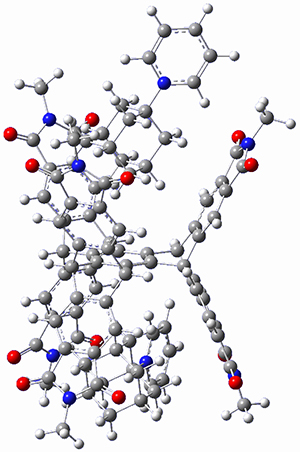
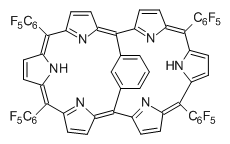
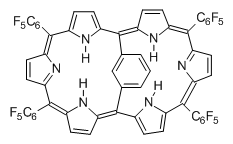
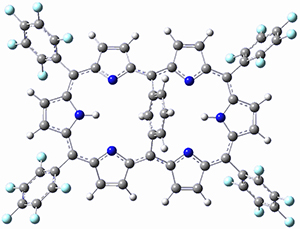
This paper presents a novel way of computing vibrational effects on chemical shifts.  Existing methods generally compute such effects by displacing the coordinates along the normal modes to create PESs, computing the vibrational wavefunctions, computing chemical shifts for the displaced coordinates, and computing the chemical shifts as expectation values. However, it can be challenging to use this approach on low frequency modes since they require relatively large displacements which tend to distort the molecule in unphysical ways. This problem can, in part, be solved by using internal coordinates but results can wary greatly depending on which internal coordinates one chooses.  

Kwan and Liu propose instead to perform a short (125 fs) B3LYP/MIDI! quasi-classical MD simulation "along" each normal mode and then compute an average chemical shift based on the trajectory. The MD simulation is "quasi-classical" in the sense that it is initialized based in the vibrational harmonic oscillator energy levels. The energy level is randomly selected from a Boltzmann distribution and 25 trajectories were found to be sufficient. Since the forces are computed at each point and used to determine the next displacement point unphysical distortions of the molecule are avoided.  Another difference is that the chemical shifts are computed using a higher level of theory (B3LYP/cc-pVDZ) than that used to construct the PES.

The various choices for method, basis set, simulation length, number of trajectories, etc is tested extensively in the supplementary materials, which also contains a more thorough description of steps in the algorithm (page 96).  Here the authors also state that they "are in the process of developing a user-friendly package for carrying out these calculations, which will be reported in due course."

Compared to the previously published methods for computing vibrational corrections this method is significantly more expensive in terms of energy and gradient evaluations.  However, I wonder if the methods can be combined such that this method is used only for lower frequency modes that can problematic for the "displacement" methods.  I also wonder if the method can be adapted to compute the anharmonic corrections to the enthalpy and entropy, which also can prove challenging for displacement-based methods.

This work is licensed under a Creative Commons Attribution 4.0

Tetrabenzo[a,f,j,o]perylene: A Polycyclic Aromatic Hydrocarbon With An Open-Shell Singlet Biradical Ground State

Liu, J.; Ravat, P.; Wagner, M.; Baumgarten, M.; Feng, X.; Müllen, K. Angew. Chem. Int. Ed. 2015, 54, 12442-12446
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Feng, Müller and co-workers have prepared a bistetracene analogue 1.¹ This molecule displays some interesting features. While a closed shell Kekule structure can be written, a biradical structure results in more closed Clar rings, suggesting that perhaps the molecule is a ground state singlet biradical. The loss of NMR signals with increasing temperature along with an EPR signal that increases with temperature both support the notion of a ground state singlet biradical with a triplet excited state. The EPR measurement suggest as singlet-triplet gap of 3.4 kcal mol^-1.

The optimized B3LYP/6-31G(d,p) geometries of the biradical singlet and triplet states are shown in Figure 1. The singlet is lower in energy by 6.7 kcal mol^-1. The largest spin densities are on the carbons that carry the lone electron within the diradical-type Kekule structures.

singlet 1

triplet 1

Figure 1. B3LYP/6-31G(d,p) optimized geometries of the biradical singlet and triplet states of 1.

References

(1) Liu, J.; Ravat, P.; Wagner, M.; Baumgarten, M.; Feng, X.; Müllen, K. "Tetrabenzo[a,f,j,o]perylene: A Polycyclic Aromatic Hydrocarbon With An Open-Shell Singlet Biradical Ground State," Angew. Chem. Int. Ed. 2015, 54, 12442-12446, DOI: 10.1002/anie.201502657.

InChIs

1: InChI=1S/C62H56/c1-33-25-35(3)51(36(4)26-33)53-45-17-13-15-19-47(45)57-56-44-24-22-42(62(10,11)12)30-40(44)32-50-54(52-37(5)27-34(2)28-38(52)6)46-18-14-16-20-48(46)58(60(50)56)55-43-23-21-41(61(7,8)9)29-39(43)31-49(53)59(55)57/h13-32H,1-12H3
InChIKey=LPRMROONCKWUEJ-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Molecular Dynamics of the Diels–Alder Reactions of Tetrazines with Alkenes and N2 Extrusions from Adducts

Törk, L.; Jiménez-Osés, G.; Doubleday, C.; Liu, F.; Houk, K. N. J. Am. Chem. Soc. 2015, 137, 4749-4758
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Houk and Doubleday report yet another example of dynamic effects in reactions that appear to be simple, ordinary organic reactions.¹ Here they look at the Diels-Alder reaction of tetrazine 1 with cyclopropene 2. The reaction proceeds by first crossing the Diels-Alder transition state 3 to form the intermediate 4. This intermediate can then lose the anti or syn N₂, through 5a or 5s, to form the product 6. The structures and relative energies, computed at M06-2X/6-31G(d), of these species are shown in Figure 1.

3 17.4	4 -33.2
5a -28.9	5s -20.0
6 -86.2

Figure 1. M06-2X/6-31G(d) optimized geometries and energies (relative to 1 + 2) of the critical points along the reaction of tetrazine with cyclopropene.

The large difference in the activation barriers between crossing 5a and 5s (nearly 9 kcal mol^-1) suggests, by transition state theory, a preference of more than a million for loss of the anti N₂ over the syn N₂. However, quasiclassical trajectory studies, using B3LYP/6-31G(d), finds a different situation. The antipathway is preferred, but only by a 4:1 ratio! This dynamic effect arises from a coupling of the v₃ mode which involves a rocking of the cyclopropane ring that brings a proton near the syn N₂ functionality, promoting its ejection. In addition, the trajectory studies find short residence times within the intermediate neighborhood for the trajectories that lead to the anti product and longer residence times for the trajectories that lead to the syn product. All together, a very nice example of dynamic effects playing a significant role in a seemingly straightforward organic reaction.

References

(1) Törk, L.; Jiménez-Osés, G.; Doubleday, C.; Liu, F.; Houk, K. N. "Molecular Dynamics of the Diels–Alder Reactions of Tetrazines with Alkenes and N₂ Extrusions from Adducts," J. Am. Chem. Soc. 2015, 137, 4749-4758, DOI: 10.1021/jacs.5b00014.

InChIs

1: InChI=1S/C2H2N4/c1-3-5-2-6-4-1/h1-2H
InChIKey=HTJMXYRLEDBSLT-UHFFFAOYSA-N

2: InChI=1S/C3H4/c1-2-3-1/h1-2H,3H2
InChIKey=OOXWYYGXTJLWHA-UHFFFAOYSA-N

4: InChI=1S/C5H6N4/c1-2-3(1)5-8-6-4(2)7-9-5/h2-5H,1H2
InChIKey=JGSMBFYJCNPYDM-UHFFFAOYSA-N

6: InChI=1S/C5H6N2/c1-4-2-6-7-3-5(1)4/h2-5H,1H2
InChIKey=RYJFHKGQZKUXEH-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Dual-Cavity Basket Promotes Encapsulation in Water in an Allosteric Fashion

Chen, S.; Yamasaki, M.; Polen, S.; Gallucci, J.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2015, 137, 12276
Contributed by Steven Bachrach
Reposted from Computational Organic Chemistry with permission

Badjic, Hadad, and coworkers have prepared ¹ an interesting host molecule that appears like two cups joined at the base, with one cup pointed up and the other pointed down. A slightly simplified analogue 1of the synthesized host is shown in Figure 1. The actual host is found to bind one molecule of 2, but does not appear to bind a second molecule. Seemingly, only one of the cups can bind a guest, and that this somehow deters a second guest from being bound into the other cup.

Figure 1. B3LYP/6-31G* optimized geometry of host molecule 1. (Visualization of this molecules and the structures below are greatly enhanced by clicking on each image which will invoke the molecular viewer Jmol.)

To address negative allosterism, the authors optimized the structure of 1 at B3LYP/6-31G* (shown in Figure 1). They then optimized the geometry with the constraint that the three arms in the top cup were ever more slightly moved inward. This had the consequential effect of moving the three arms of the bottom cup farther apart. They next optimized (at M06-2x/6-31G(d)) the structures of 1 holding one molecule of guest 2 and with two molecules of guest 2. These structures are shown in Figure 2. In the structure with one guest, the arms are brought in towards the guest for the cup where the guest is bound, and this consequently draws the arms in the other cup to be farther apart, and thereby less capable of binding a second guest. The structure with two guest shows that the arms are not able to get sufficiently close to either guest to form strong non-covalent interactions.

Figure 2. M06-2x/6-31G(d) optimized structures of 1 with one or two molecules of 2.

Thus, the negative allosterism results from a geometric change created by the induced fit of the first guest that results in an unfavorable environment for a second guest.

 

References

(1) Chen, S.; Yamasaki, M.; Polen, S.; Gallucci, J.; Hadad, C. M.; Badjić, J. D. "Dual-Cavity Basket Promotes Encapsulation in Water in an Allosteric Fashion," J. Am. Chem. Soc. 2015, 137, 12276-12281, DOI:10.1021/jacs.5b06041.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Switching between Aromatic and Antiaromatic 1,3-Phenylene-Strapped [26]- and [28]Hexaphyrins upon Passage to the Singlet Excited State

Sung, Y. M.; Oh, J.; Kim, W.; Mori, H.; Osuka, A.; Kim, D. J. Am. Chem. Soc. 2015, 137, 11856
Contributed by Steven Bachrach.

Reposted from Computational Organic Chemistry with permission

What is the relationship between a ground state and the first excited triplet (or first excited singlet) state regarding aromaticity? Baird¹ argued that there is a reversal, meaning that a ground state aromatic compound is antiaromatic in its lowest triplet state, and vice versa. It is suggested that the same reversal is also true for the second singlet (excited singlet) state.

Osuka, Sim and coworkers have examined the geometrically constrained hexphyrins 1 and 2.² 1 has 26 electrons in the annulene system and thus should be aromatic in the ground state, while 2, with 28 electrons in its annulene system should be antiaromatic. The ground state and lowest triplet structures, optimized at B3LYP/6-31G(d,p), of each of them are shown in Figure 1.

1

2

11	12
31	32

Figure 1. B3LYP/6-31G(d,p) optimized geometries of 1 and 2.

NICS computations where made in the centers of each of the two rings formed by the large macrocycle and the bridging phenyl group (sort of in the centers of the two lenses of the eyeglass). The NICS values for 1are about -15ppm, indicative of aromatic character, while they are about +15ppm for 2, indicative of antiaromatic character. However, for the triplet states, the NICS values change sign, showing the aromatic character reversal between the ground and excited triplet state. The aromatic states are also closer to planarity than the antiaromatic states (which can be seen by clicking on the images in Figure 1, which will launch the JMol applet so that you can rotate the molecular images).

They also performed some spectroscopic studies that support the notion of aromatic character reversal in the excited singlet state.

References

(1) Baird, N. C. "Quantum organic photochemistry. II. Resonance and aromaticity in the lowest ³ππ* state of cyclic hydrocarbons," J. Am. Chem. Soc. 1972, 94, 4941-4948, DOI: 10.1021/ja00769a025.

(2) Sung, Y. M.; Oh, J.; Kim, W.; Mori, H.; Osuka, A.; Kim, D. quot;Switching between Aromatic and Antiaromatic 1,3-Phenylene-Strapped [26]- and [28]Hexaphyrins upon Passage to the Singlet Excited State," J. Am. Chem. Soc. 2015, 137, 11856-11859, DOI: 10.1021/jacs.5b04047.

InChIs

1: InChI=1S/C60H18F20N6/c61-41-37(42(62)50(70)57(77)49(41)69)33-23-8-4-19(81-23)31-17-2-1-3-18(16-17)32(21-6-10-25(83-21)35(29-14-12-27(33)85-29)39-45(65)53(73)59(79)54(74)46(39)66)22-7-11-26(84-22)36(40-47(67)55(75)60(80)56(76)48(40)68)30-15-13-28(86-30)34(24-9-5-20(31)82-24)38-43(63)51(71)58(78)52(72)44(38)64/h1-16,85-86H/b31-19+,31-20+,32-21+,32-22+,33-23+,33-27+,34-24+,34-28+,35-25+,35-29+,36-26+,36-30+
InChIKey=TUOMWLSCXXODFY-CQGNQUHXSA-N

2: InChI=1S/C60H20F20N6/c61-41-37(42(62)50(70)57(77)49(41)69)33-23-8-4-19(81-23)31-17-2-1-3-18(16-17)32(21-6-10-25(83-21)35(29-14-12-27(33)85-29)39-45(65)53(73)59(79)54(74)46(39)66)22-7-11-26(84-22)36(40-47(67)55(75)60(80)56(76)48(40)68)30-15-13-28(86-30)34(24-9-5-20(31)82-24)38-43(63)51(71)58(78)52(72)44(38)64/h1-16,81-84H/b31-19+,31-20+,32-21+,32-22+,33-23+,33-27+,34-24+,34-28+,35-25+,35-29+,36-26+,36-30+
InChIKey=KTIAGNMFTAGKFJ-CQGNQUHXSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

A Local Variant of the Conductor-Like Screening Model for Fragment-Based Electronic-Structure Methods

Albrecht Goez and Johannes Neugebauer J. Chem. Theory Comput., Article ASAP, DOI: 10.1021/acs.jctc.5b00832
Contributed by Christoph Jacob
 
Fragment-based methods nowadays make it possible to perform quantum-chemical calculations for rather large biomolecules, for instance light-harvesting protein systems [1]. Such methods are based on the idea of splitting a protein into smaller fragments, such as its constituting amino acids. This leads to a linear scaling of the computational effort with the size of protein. Popular examples of fragment-based electronic structure methods include the fragment molecular orbital (FMO) method [2] and a generalization of the frozen-density embedding scheme (3-FDE) [3].

In a recent article in JCTC, Goez and Neugebauer from the University of Münster (Germany) address an additional bottleneck that appears in such calculations. Usually, it is necessary to include a solvent environment in the calculations, in particular if charged amino-acid side chains are present. The simplest way of doing so are continuum solvation models, such as COSMO or PCM. These models represent the solvent in terms of apparent charges on the surface of a cavity enclosing the protein. However, for proteins the number of apparent surfaces charges becomes rather large - for ubiquitin, a protein with only 78 amino acids, already 20,000 charges are needed. Updating these apparent surface charges involves solving a linear system of equations of size 20,000 x 20,000. When doing so in each SCF cycle for each of the fragments, the continuum solvation model will become the bottleneck of the calculation.

To solve this problem, Goez and Neugebauer developed a local variant of the COSMO model (LocCOSMO). In each fragment calculation, they update only those apparent surface charges that are close to this fragment. This reduces the computational effort significantly, but because every fragment is updated at some point it will eventually result in the same final result. This is demonstrated by the authors for several test cases. They can reduce the computational time required for a 3-FDE calculation of ubiquitin in a solvent environment by a factor of 30, without compromising the quality of the result.

The efficient combination of fragment-based quantum chemistry with continuum solvation models  provides an important tool for studies of biomolecules. It will make such calculations more robust by alleviating convergence problems for charged amino acids and will allow for a more realistic inclusion of protein environments in studies of spectroscopic properties of chromophores in biomolecular systems.

References:

[1] A. Goez, Ch. R. Jacob, J. Neugebauer, “Modeling environment effects on pigment site energies: Frozen density embedding with fully quantum-chemical protein densities”, Comput. Theor. Chem. 1040–1041, 347–359 (2014).
[2] D. G. Fedorov, K. Kitaura, “Extending the Power of Quantum Chemistry to Large Systems with the Fragment Molecular Orbital Method”, J. Phys. Chem. A 111, 6904–6914 (2007).
[3] Ch. R. Jacob, L. Visscher, “A subsystem density-functional theory approach for the quantum chemical treatment of proteins”, J. Chem. Phys. 128, 155102 (2008).