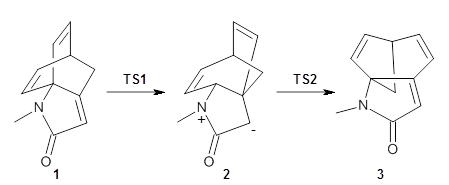Hiroya Nakata, Dmitri G. Fedorov, Takeshi Nagata, Kazuo Kitaura, and Shinichiro Nakamura. Journal of Chemical Theory and Computation 2015, 11, 3053−3064
Contributed by +Jan Jensen
I am highlighting this paper because it is the first paper I have come across that reports the optimized TS, free energy barrier, and IRC for an enzymatic reaction using an all-QM description of the entire enzyme.
The underlying method is the frozen domain with dimers (FDD) formulation of the fragment molecular orbital method (FMO) implemented in the GAMES program. The FMO is fragmentation method and in the FDD formulation the system is divided into three domain: A) an active domain where the both the geometry and density are allowed to change, B) a polarizable buffer where only the density is allowed to change and F) a frozen domain where neither is allowed to change. The latter restraints means that the fragments in the frozen domain only have to be calculated once.
This paper presents the implementation of the fully analytic gradient and Hessian at the RHF level and the interface to the IRC methodology in GAMESS. (The interface to the TS-optimization code was reported previously using a different variant of FMO.) In this approach only the Hessian of the active domain is computed.
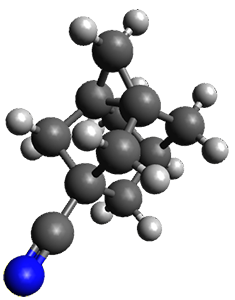
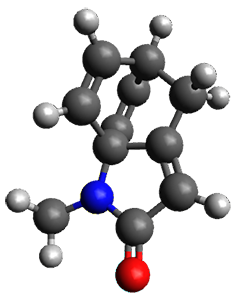
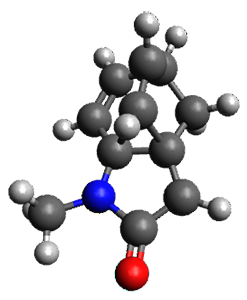
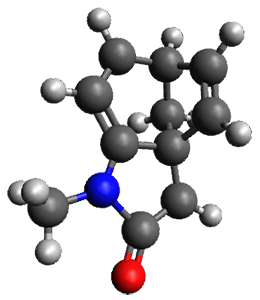
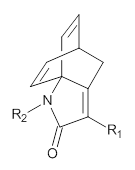
The method is then applied to the keo-enol tautomerization of phosphoglycolohydroxamic acid (PGH) by triosephosphate isomerase (TIM). The active domain is PGH and the proton donor Glu410 while the polarizable buffer is any residue or water molecule within 5.2 Å of the active domain, which were both treated at the RHF/6-31G(d) + dispersion level of theory. The frozen domain, i.e. the rest of the TIM monomer, is treated at the RHF/STO-3G level of theory and the entire system is comprised of 9227 atoms.
The workflow was at follows using 128 2.93 GHz Xeon cores:
1. Constrained optimization to obtain TS guess (12 hrs)
2. Hessian calculation (24 hrs)
3. TS optimization (12 hrs)
4. Hessian calculation (24 hrs)
5. IRC calculations (16 points) in each direction (42 hrs)
6. Optimization of reactants and products starting from last IRC points (12 hrs each)
7. Hessian calculation for reactant and products (24 hrs each)
Of course, at this level of theory and with such a small active domain the resulting free energy barrier (21.4 kcal/mol) is considerably different from the experimental value (14 kcal/mol) but this is only a proof-of-concept study.
An important next step for FMO studies of enzyme catalysis will be the implementation of a mixed DFT/RHF-D model where all or part of the active domain can be treated with DFT. The computational cost-increase associated with using DFT could be off-set by using, for example, HF-3c for the non-reactive part of of the active region as well as the buffer region since this method gives excellent structures as low computational cost.
I thank +Casper Steinmann for alerting me to this article

This work is licensed under a Creative Commons Attribution 4.0
Contributed by +Jan Jensen
Reprinted (adapted) with permission from J. Chem. Theory Comput. 2015, 11, 3053−3064. Copyright (2015) American Chemical Society
I am highlighting this paper because it is the first paper I have come across that reports the optimized TS, free energy barrier, and IRC for an enzymatic reaction using an all-QM description of the entire enzyme.
The underlying method is the frozen domain with dimers (FDD) formulation of the fragment molecular orbital method (FMO) implemented in the GAMES program. The FMO is fragmentation method and in the FDD formulation the system is divided into three domain: A) an active domain where the both the geometry and density are allowed to change, B) a polarizable buffer where only the density is allowed to change and F) a frozen domain where neither is allowed to change. The latter restraints means that the fragments in the frozen domain only have to be calculated once.
This paper presents the implementation of the fully analytic gradient and Hessian at the RHF level and the interface to the IRC methodology in GAMESS. (The interface to the TS-optimization code was reported previously using a different variant of FMO.) In this approach only the Hessian of the active domain is computed.
The method is then applied to the keo-enol tautomerization of phosphoglycolohydroxamic acid (PGH) by triosephosphate isomerase (TIM). The active domain is PGH and the proton donor Glu410 while the polarizable buffer is any residue or water molecule within 5.2 Å of the active domain, which were both treated at the RHF/6-31G(d) + dispersion level of theory. The frozen domain, i.e. the rest of the TIM monomer, is treated at the RHF/STO-3G level of theory and the entire system is comprised of 9227 atoms.
The workflow was at follows using 128 2.93 GHz Xeon cores:
1. Constrained optimization to obtain TS guess (12 hrs)
2. Hessian calculation (24 hrs)
3. TS optimization (12 hrs)
4. Hessian calculation (24 hrs)
5. IRC calculations (16 points) in each direction (42 hrs)
6. Optimization of reactants and products starting from last IRC points (12 hrs each)
7. Hessian calculation for reactant and products (24 hrs each)
Of course, at this level of theory and with such a small active domain the resulting free energy barrier (21.4 kcal/mol) is considerably different from the experimental value (14 kcal/mol) but this is only a proof-of-concept study.
An important next step for FMO studies of enzyme catalysis will be the implementation of a mixed DFT/RHF-D model where all or part of the active domain can be treated with DFT. The computational cost-increase associated with using DFT could be off-set by using, for example, HF-3c for the non-reactive part of of the active region as well as the buffer region since this method gives excellent structures as low computational cost.
I thank +Casper Steinmann for alerting me to this article

This work is licensed under a Creative Commons Attribution 4.0