Phase Transition of [2,2]-Paracyclophane – An End to an Apparently Endless Story

Wolf, H.; Leusser, D.; Jørgensen, M. R. V.; Herbst-Irmer, R.; Chen, Y.-S.; Scheidt, E.-W.; Scherer, W.; Iversen, B. B.; Stalke, D. Chem. Eur. J. 2014, 20, 7048–7053
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

The structure of [2,2]paracyclophane 1 has been somewhat controversial for some time. Early x-ray structures indicated that the molecule was quite symmetric, D_2h with the phenyl rings and the ethyl bridges eclipsed. Subsequent low-T experiments suggested a lower symmetry form D₂ with a twist that relieves some of the unfavorable eclipsing interactions in the ethano bridges. High-level computations by Grimme¹ and then some by myself² indicated that the D₂ structure is the lowest energy conformation, with however a low barrier through the D_2h structure.

The suggestion of the D₂ minimum was vehemently criticized by Dodziuk, et al. on the basis of NMR analysis.³

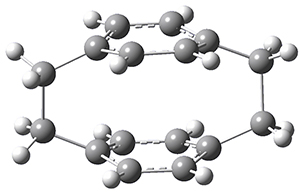
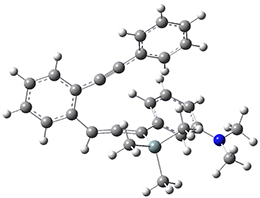
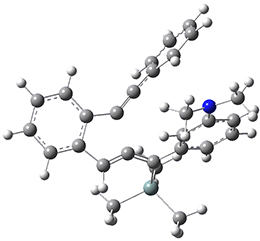
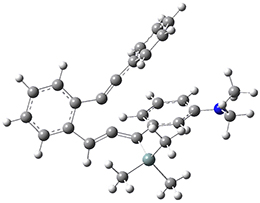
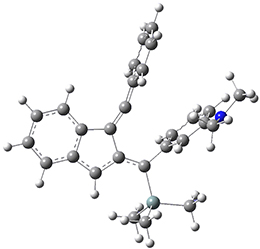
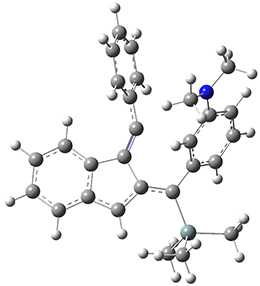
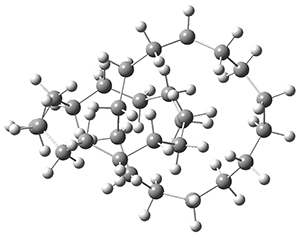
Now, a low temperature x-ray experiment of 1 brings clarity to the situation.⁴ (The introduction provides a nice summary of the previous 70 year history regarding the structure of 1.) At temperatures below 45 K, 1 is found as a single structure of D₂ symmetry (with space group P4n2). The structure is shown in Figure 1. A phase change occurs at about 45 K, and above 60 K the crystal has P4₂/mnm symmetry. The structure of 1 at the high temperature appears as D_2h with somewhat broader thermal motion of the ethano carbons than the phenyl carbons. The low T structure is in excellent accord with the previous theoretical studies, and the phase transition helps bring into accord all of the previous x-ray crystallographic work.

Figure 1. X-ray structure at 15K of 1.

References

(1) Grimme, S. "On the Importance of Electron Correlation Effects for the π-π Interactions in Cyclophanes," Chemistry Eur. J. 2004, 10, 3423-3429, DOI: 10.1002/chem.200400091.

(2) Bachrach, S. M. "DFT Study of [2.2]-, [3.3]-, and [4.4]Paracyclophanes: Strain Energy, Conformations, and Rotational Barriers," J. Phys. Chem. A 2011, 115, 2396-2401, DOI: 10.1021/jp111523u.

(3) Dodziuk, H.; Szymański, S.; Jaźwiński, J.; Ostrowski, M.; Demissie, T. B.; Ruud, K.; Kuś, P.; Hopf, H.; Lin, S.-T. "Structure and NMR Spectra of Some [2.2]Paracyclophanes. The Dilemma of [2.2]Paracyclophane Symmetry," J. Phys. Chem. A 2011, 115, 10638-10649, DOI: 10.1021/jp205693a.

(4) Wolf, H.; Leusser, D.; R. V. Jørgensen, M.; Herbst-Irmer, R.; Chen, Y.-S.; Scheidt, E.-W.; Scherer, W.; Iversen, B. B.; Stalke, D. "Phase Transition of [2,2]-Paracyclophane – An End to an Apparently Endless Story," Chem. Eur. J. 2014, 20, 7048–7053, DOI: 10.1002/chem.201304972.

InChIs

1: InChI=1S/C16H16/c1-2-14-4-3-13(1)9-10-15-5-7-16(8-6-15)12-11-14/h1-8H,9-12H2
InChIKey=OOLUVSIJOMLOCB-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Monte Carlo Free Ligand Diffusion with Markov State Model Analysis and Absolute Binding Free Energy Calculations

Takahashi, Ryoji, Víctor A. Gil, and Victor Guallar  Journal of Chemical Theory and Computation 2014, 10, 282−288.

Contributed by +Jan Jensen

This study uses Monte Carlo (MC) sampling, and a Markov state model analysis of the resulting trajectories, to compute absolute binding free energies for four benzamidine ligands binding to trypsin that are in good agreement with experiment.  The measured binding free energies for the same ligand vary a bit and the mean absolute deviation ranges from 0.9 to 1.4 kcal/mol.

The binding free energy for each ligand is derived from a Markov state model analysis of 840 MC trajectories constructed using six different random initial ligand positions - all well away from the protein surface. Each MC trajectory is constructed using the protein energy landscape exploration (PELE) method. There are three kinds of PELE MC moves: (1) the ligand can be translated or rotated rigidly, (2) the internal ligand geometry can be changed using a ligand-specific rotamer library, and (3) all protein atoms are displaced along a randomly picked mode derived from an anisotropic network model followed by minimization of all all atoms except the $\alpha$-carbons.

After each move is made the side-chain orientations close to the ligands are sampled from a rotamer library followed my an OPLS-AA/SGB energy minimization of all atoms affected by the move. The resulting "super move" is accepted or rejected based on a Metropolis criterion.

The total simulation time for a ligand is about 1 week using 64 cores. However, the binding site of each ligand could be identified using only 20-30 trajectories in 5-10 CPU hours.  In fact, such a binding site search can be performed using the PELE web server developed by the authors.

With its use of "super moves" with extensive energy minimization this method strikes me as an excellent way to generate snapshots for QM/MM calculations and it seems to me it could be easily adapted to look at enzyme catalysis.


This work is licensed under a Creative Commons Attribution 4.0 International License.

Polytwistane

Barua, S. R.; Quanz, H.; Olbrich, M.; Schreiner, P. R.; Trauner, D.; Allen, W. D. Chem. Eur. J. 2014, 20, 1638-1645
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Twistane 1 is a more strained isomer of adamantane 2. The structure of 1 is shown in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized structure of 1.

Adamantane is the core structure of diamond, which can be made by appending isobutene groups onto adamantane. In an analogous fashion, twistane can be extended in a linear way by appending ethano groups in a 1,4-bridge. Allen, Schreiner, Trauner and co-workers have examined this “polytwistane” using computational techniques.¹ They examined a (CH)₂₃₆ core fragment of polytwistane, with the dangling valences at the edges filled by appending hydrogens, giving a C₂₃₆H₂₄₂ compound. This compound was optimized at B3LYP/6-31G(d) and shown in Figure 2a. (Note that I have zoomed in on the structure, but by activating Jmol – click on the figure – you can view the entire compound.) A fascinating feature of polytwistane is its helical structure, which can be readily seen in Figure 2b. A view down the length of this compound, Figure 2c, displays the opening of this helical cylinder; this is a carbon nanotube with an inner diameter of 2.6 Å.

(a)

(b)

(c)

Figure 2. B3LYP/6-31G(d) structure of the C₂₃₆H₂₄₂ twistane. (a) A zoomed in look at the structure. This structure links to the Jmol applet allowing interactive viewing of the molecule – you should try this! (b) a side view clearly showing its helical nature. (c) A view down the twistane showing the nanotube structure.

Though the molecule looks quite symmetric, each carbon is involved in three C-C bonds, and each is of slightly different length. The authors go through considerable detail about addressing the symmetry and proper helical coordinates of polytwistane. They also estimate a strain energy of about 1.6 kcal mol^-1 per CH unit. This modest strain, they believe, suggests that polytwistanes might be reasonable synthetic targets.

References

(1) Barua, S. R.; Quanz, H.; Olbrich, M.; Schreiner, P. R.; Trauner, D.; Allen, W. D. "Polytwistane," Chem. Eur. J. 2014, 20, 1638-1645, DOI: 10.1002/chem.201303081.

InChIs

1: InChI=1S/C10H16/c1-2-8-6-9-3-4-10(8)5-7(1)9/h7-10H,1-6H2
InChIKey=AEVSQVUUXPSWPL-UHFFFAOYSA-N

2: InChI=1S/C10H16/c1-7-2-9-4-8(1)5-10(3-7)6-9/h7-10H,1-6H2
InChIKey=ORILYTVJVMAKLC-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Quantification of Nonstatistical Dynamics in an Intramolecular Diels–Alder Cyclization without Trajectory Computation

Samanta, D.; Rana, A.; Schmittel, M. J. Org. Chem. 2014, 79, 2368

Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Demonstrating the occurrence of non-statistical dynamics generally has been accomplished through trajectory studies. These trajectory studies are often quite computationally demanding, requiring many trajectories, often of long duration, with molecules that are typically not small! Schmittel and co-workers present a case where their evidence for non-statistical dynamics rests not on trajectory studies but a combination of experimental product distributions and free energy of activation computations.¹

For the Schmittel C²-C⁶ cyclization taking 1 into 5¸Schmittel has located no concerted transition state, but rather two different transition states 2 and 2’, leading to a common intermediate diradical 3. Then there are two different transition states 4 and 4’ leading to the two regioisomeric products 5 and 5’. The BLYP/6-31G* structures and relative free energies are shown in Figure 1.

1 0.0
2 19.4	2’ 20.2
3 13.3
4 16.5	4’ 15.4
5 -6.3	5’ -14.3

Figure 1. BLYP/6-31G*geometries and relative free energies (kcal mol^-1) of the critical points along the reaction 1 → 5.

If transition state theory (TST) holds here, the rate limiting step is the first set of transition states, and the product distribution should be dictated by the second set of transition states. Since 4’ is lower in energy than 4, TST predicts that 5’ should be the major product. However, the experiments show that the ratio 5:5’ ranges from 1.48 at 30 °C to 1.65 at 60 °C, with the ratio decreasing a bit at higher temperatures still.

Examination of the potential energy surfaces in the neighborhoods of the transition states and the intermediate show a couple of interesting features. First, there is a large barrier separating 2 and 2’ and this precludes the concerted pathway. Second, the minimum energy path forward from 2 requires a sharp turn to proceed to the intermediate 3. Schmittel suggests that this surface supports the notion of some direct reaction paths from 2 avoiding the intermediate 3 and directly over transition state 4’. Schmittel offers a simple formula for predicting the percentage of the products formed from a non-statistical pathway:

X_NSQ₁ + X_SQ₂ = Q_exp

where X_NS is the mole fraction following non-statistical pathways and X_S is the fraction following a statistical pathway and Q_exp is the experimental mole ratio and Q₁ is the partitioning at the first set of TSs and Q₂ is the partitioning at the second set of TSs. While this approach is certainly much simpler than performing molecular dynamics, it does require experimental values. According to this model, the above reaction follows non-statistical dynamics about 75% of the time.

References

(1) Samanta, D.; Rana, A.; Schmittel, M. "Quantification of Nonstatistical Dynamics in an Intramolecular Diels–Alder Cyclization without Trajectory Computation," J. Org. Chem. 2014, 79, 2368-2376, DOI:10.1021/jo500035b.

InChIs

1: InChI=1S/C28H29NSi/c1-29(2)27-17-11-16-26(22-27)28(30(3,4)5)21-20-25-15-10-9-14-24(25)19-18-23-12-7-6-8-13-23/h6-17,20,22H,1-5H3
InChIKey=CKQXQJAGCGSOOP-UHFFFAOYSA-N

5: InChI=1S/C28H29NSi/c1-29(2)24-17-11-16-22-27(24)25(19-12-7-6-8-13-19)26-21-15-10-9-14-20(21)18-23(26)28(22)30(3,4)5/h6-17H,18H2,1-5H3
InChIKey=OFALZDSJOVLMHZ-UHFFFAOYSA-N

5′: InChI=1S/C28H29NSi/c1-29(2)21-15-16-23-24(18-21)28(30(3,4)5)25-17-20-13-9-10-14-22(20)27(25)26(23)19-11-7-6-8-12-19/h6-16,18H,17H2,1-5H3
InChIKey=UQRNTADMKHTLNR-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

How Small Can a Catenane Be?

Feng, X.; Gu, J.; Chen, Q.; Lii, J.-H.; Allinger, N. L.; Xie, Y.; Schaefer, H. F. J. Chem. Theor. Comput. 2014, 10, 1511-1517
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

“How small can a catenane be?” This question is asked by Schaefer, Allinger and colleagues and answered (well, almost answered) using computations.¹ Catenanes are linked rings. The catenanes examined here are two linked saturated hydrocarbon rings, each of the same size. The rings examined have 11 to 18 carbon atoms. The geometries were optimized with D₂ symmetry, where either the closest approach between the two rings are two carbon atoms or the midpoint of two C-C bonds. The former turn out to be lower in energy. Geometries were optimized with MP2, B3LYP, BP86 or M06-2X with the DZP++ basis set. There is little geometric dependence on computational method. The optimized geometry of the catenane with 14 carbons is shown in Figure 1.

Figure 1. Optimized geometry of the 14-carbon catenane. (Be sure to click on this structure to view the molecule in 3-D; you will have to allow Jmol to download and run!)

To cut to the chase, as the rings get smaller they observe a lengthening of the C-C bonds at the intersection. With the 14-carbon catenane they observe a significant increase in the bond length near the intersection, suggesting a dramatic instability. This is also seen in the change in the energy per C as the rings get smaller; a large increase in energy per C is seen at the transition from 14 to 13 carbons. This all points toward the 14-carbon catenane as the smallest one that might be stable.

(I thank Prof. Schaefer and colleagues for providing me with the coordinates of the 14-carbon catenane.)

References

(1) Feng, X.; Gu, J.; Chen, Q.; Lii, J.-H.; Allinger, N. L.; Xie, Y.; Schaefer, H. F. "How Small Can a Catenane Be?," J. Chem. Theor. Comput. 2014, 10, 1511-1517, DOI: 10.1021/ct400926p

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.