Validation Challenge of Density-Functional Theory for Peptides—Example of Ac-Phe-Ala5-LysH+

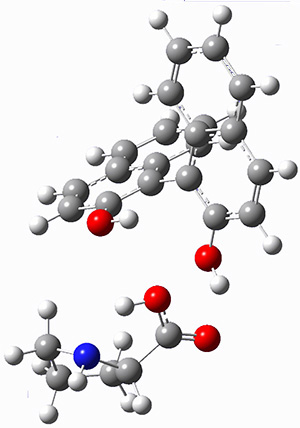
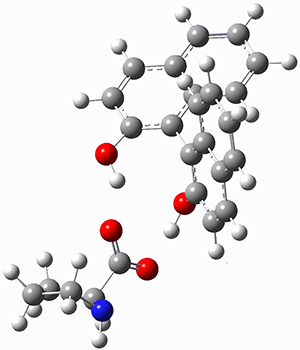
Mariana Rossi, Sucismita Chutia, Matthias Scheffler, and Volker Blum J. Phys. Chem. A 2014 ASAP
Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission

Weak interactions are difficult to model in general; there are some DFT functional which do a reasonable job on hydrogen bonding (e.g. PBE[1,2]), and there have been a number of interesting developments in the modelling of van der Waals (dispersion) forces, which I will write about in future.

A recent paper in J. Phys. Chem A by Rossi et al. (available on-line[3] and part of an on-going series of studies on peptides in DFT) gives an excellent discussion of one avenue of work pushing towards accuracy for weak bonds. The approach used for dispersion is efficient and promising (the TS vdW[4] and MBD[5] method), but there are still questions that remain.

The paper uses DFT and enhancements (hybrid functionals and dispersion corrections) to study a large peptide with around 100 atoms, for which there is excellent experimental information available[6] (in particular, the data is from the gas phase, which DFT can easily compare to). They use the FHI-aims code[7], which is a relatively new all-electron code with numerical atomic orbitals as a basis set. An important question that must be asked about this type of basis concerns basis-set superposition error (an error in energy normally found when comparing fragments of a system to the complete system, but which will have some effect when comparing compact conformers to sparse conformers). This is not discussed in the paper, though previous work has shown that for the higher accuracy basis used (tier-2) BSSE is not a dominant error; moreover, BSSE within a molecule will be a smaller effect than between molecules.

A previous study of the peptide fragment[8] found that 17 different GGAs failed to reproduce the experimental ordering of the four lowest energy conformers; Rossi et al find that hybrid functionals, dispersion and vibrational effects are needed to get this correct. However, Rossi et al. find that hybrid DFT with dispersion finds the right family of structures to be lowest in energy.

There are a number of questions that are raised by the study:

• What would the effect of a different hybrid functional be ?
• What would the effect of a different dispersion scheme be ?
• Are the vibrational data accurate enough ? (They were calculated with PBE and vdW – no hybrid functional and the less accurate dispersion approach; the authors acknowledge the difficulty of vibrational calculations, and did do one with PBE0+vdW though it gave no better agreement with experiment)

There are many different hybrid functionals available, most of which are parameterised for specific purposes (be that a specific system or to fit specific limits). As the most expensive part of the calculations done by Rossi et al. is the exchange (as is often the case) it is reasonable that they have not tested this extensively, but they do note that changing to HSE06 changes the energies between helical and non-helical conformers by ~20meV (compared to energy differences between families of 50-100meV, so it’s not insignificant).

I would be most interested to see the effect of the vdW-DF functionals[9] (I should note that I collaborated on a widely-cited study of the effects of tuning the exchange functional used with the vdW-DF functional[10]). These functionals take a completely different approach to dispersion to the TS approach (or the Grimme DFT-D approach) and would give an important view on the effects of dispersion.

It’s really good to see studies like these, pushing forward the accuracy that can be achieved by DFT, testing weak interactions, and being honest about how effective different methods are. But there is still more work to be done.

[1] J. Phys. Chem. A 108, 5692 (2004) 10.1021/jp0377073
[2] J. Phys.: Condens. Matter 20 294201 (2008) 10.1088/0953-8984/20/29/294201
[3] J. Phys. Chem. A (2014) 10.1021/jp412055r
[4] Phys. Rev. Lett. 102, 073005 (2009) 10.1103/PhysRevLett.102.073005
[5] Phys. Rev. Lett. 108, 236402 (2012) 10.1103/PhysRevLett.108.236402
[6] J. Am. Chem. Soc. 129, 13820 (2007) 10.1021/ja076507s
[7] Comp. Phys. Commun. 180, 2175 (2009) 10.1016/j.cpc.2009.06.022
[8] Chem. Eur. J 18, 12941 (2012) 10.1002/chem.201202068
[9] Phys. Rev. Lett. 92, 246401 (2004) 10.1103/PhysRevLett.92.246401
[10] J. Phys.: Condens. Matter 22 022201 (2010) 10.1088/0953-8984/22/2/022201

Induced-fit catalysis of corannulene bowl-to-bowl inversion

Juríček, M.; Strutt, N. L.; Barnes, J. C.; Butterfield, A. M.; Dale, E. J.; Baldridge, K. K.; Stoddart, J. F.; Siegel, J. S. Nat. Chem. 2014, 6, 222

Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

The concept of complementarity between enzyme and substrate, especially the transition state for reactions at the substrate, is a key element of Pauling’s model for enzymatic activity. Koshland’s “induced fit” modification suggests that the enzyme might change its structure during the binding process to either destabilize the reactant or help stabilize the TS. These concepts are now tested in a very nice model by Stoddart, Siegel and coworkers.¹

Stoddart recently reported the host compound ExBox⁴⁺ 1 and demonstrated that it binds planar polycyclic aromatic hydrocarbons.² (I subsequently reported DFT computations on this binding.) The twist in this new paper is the binding of corranulene 2 inside ExBox⁴⁺ 1. Corranulene is bowl-shaped, with a bowl inversion barrier of 11.5 kcal mol^-1 (10.92 kcal mol^-1 at B97D/Def2-TZVPP).

The corranulene bowl is too big to fit directly into 1 without some distortions. The x-ray structure of the complex of 1 with 2 inside shows the width of 1 expanding by 0.87 Å and the bowl depth of 2decreasing by 0.03 Å. The B97D/Def2-TZVPP optimized geometry of this complex (shown in Figure 1) shows similar distortions – the width of 1 increases by 0.37 Å (gas) or 0.29 Å (acetone solution), while the bowl depth of 2 decreases by 0.03 Å (gas) or 0.02 Å (solution).

ground state

transition state

Figure 1. B97D/Def2-TZVPP optimized geometries of the complex of 2 inside 1 (a) ground state and (b) transition state.

The calculated structure of the bowl inversion transition state of 2 inside of 1 is shown in Figure 1. 2 is planar at the TS. The experimental inversion barrier (determined by variable temperature NMR line shift analysis) is 7.88 kcal mol^-1, while the calculated barrier is 8.77 kcal mol^-1. The reduction in the bowl inversion barrier of 2 inside of 1 is therefore about 2.5 kcal mol^-1. The authors argue that this barrier reduction can be attributed to about 0.5 kcal mol^-1 of destabilization of the ground state of 2 along with 2 kcal mol^-1 of stabilization of the transition state afforded by the host. This study thus confirms the notions of a host reducing a barrier (through both transition state stabilization and ground state destabilization) and induced fit.

References

(1) Juríček, M.; Strutt, N. L.; Barnes, J. C.; Butterfield, A. M.; Dale, E. J.; Baldridge, K. K.; Stoddart, J. F.; Siegel, J. S. "Induced-fit catalysis of corannulene bowl-to-bowl inversion," Nat. Chem. 2014, 6, 222-228, DOI: 10.1038/nchem.1842.

(2) Barnes, J. C.; Juríček, M.; Strutt, N. L.; Frasconi, M.; Sampath, S.; Giesener, M. A.; McGrier, P. L.; Bruns, C. J.; Stern, C. L.; Sarjeant, A. A.; Stoddart, J. F. "ExBox: A Polycyclic Aromatic Hydrocarbon Scavenger," J. Am. Chem. Soc. 2012, 135, 183-192, DOI: 10.1021/ja307360n.

(3) Bachrach, S. M. "DFT Study of the ExBox·Aromatic Hydrocarbon Host–Guest Complex," J. Phys. Chem. A 2013, 117, 8484-8491, DOI: 10.1021/jp406823t.

InChIs

1: InChI=1S/C48H40N4/c1-2-38-4-3-37(1)33-49-25-17-45(18-26-49)41-9-11-43(12-10-41)47-21-29-51(30-22-47)35-39-5-7-40(8-6-39)36-52-31-23-48(24-32-52)44-15-13-42(14-16-44)46-19-27-50(34-38)28-20-46/h1-32H,33-36H2/q+4
InChIKey=ZMELWAYDWQWNOQ-UHFFFAOYSA-N

2: InChI=1S/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey=VXRUJZQPKRBJKH-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Comparison of Ab Initio, DFT and Semiempirical QM/MM approaches for description of catalytic mechanism of hairpin ribozymes

Vojte Mlynsky, Pavel Banas, Jiri Sponer, MarcW. van der Kamp, Adrian J. Mulholland, and Michal Otyepka, Journal of Computational and Theoretical Chemistry, 2014, DOI:10.1021/ct401015e

Contributed by Esteban Vohringer-Martinez

I enjoyed very much reading this paper where the authors report a very interesting study in which the performance of semiempirical methods in QM/MM calculations is addressed in detail.

The reaction under study is the reversible phosphodiester bond cleavage and ligation in hairpin ribozymes. These ribozymes belong to a small group which catalyze the reaction without any metal ion at comparable rates.

From experimental evidence and previous theoretical calculations it was known that there are two main players in the catalytic reaction: A38 and G8; two neighbouring bases to the phosphodiester bond to be cleaved between the Adenine -1 and Guanine +1 (see scheme below). However which was not clear from the theoretical studies nor the experiment is the protonation state for the A38 and G8 bases. The experimental studies showed a pH dependence in the catalytic activity of the ribozyme implying different catalytic activity as a function of protonation state.

To account for different protonation states the authors studied two reaction mechanisms: the mono anionic one (top) where only the phosphatediester group is deprotonated and the dianionic mechanism where the G8 bases is also deprotonated (bottom). In both mechanism they assumed the A38 to be protonated (see reaction scheme).

The energetics of the reaction are followed along two reaction coordinates represented by a linear combination of the cleaving and forming bonds (d1 and d2) in the proton transfer step and the oxygen-phosphor distance as shown in the scheme. 

The energies were calculated with the SCS(spin component scaled)-MP2  single point energy calculations (CBS limit) on BLYP optimized geometries (6-31G(d,p) in a QM/MM electrostatic embedding with the AMBER99sb force field.  The test methods include the MPW1K hybrid functional, the BLYP GGA DFT functional and the semiempirical methods AM1/dPhoT and SCC-DFTBPR.

For me the main finding of this paper is that Ab-Initio and all DFT methods predict a concerted nucleophilic and proton transfer mechanism whereas both semiempirical methods yield a sequential mechanism where first the proton is transferred and then the nucleophilic attack takes place. Interestingly both semiempirical methods yield a stable intermediate in the dianionic mechanism after the proton transfer step which is not present in the ab-initio and DFT results. 

These result raise doubts about the ability of semiempirical methods to provide correct structures and reaction mechanisms in enzyme catalysis and suggest that a careful calibration of these methods for each system should be performed prior to its usage. 

One additional aspect to consider is that the activation barrier of the semiempirical methods were close to the ab-initio, DFT methods and experiment. However, a match of barrier heights as shown in this study does not guarantee a correct reaction mechanism.

Finally, the authors also compare their results to free energy calculations employing semiempirical methods. But, as the authors also conclude the almost negligible entropy contribution they report should be taken with care due to the very short sampling time of only 50ps.

Diamond: Electronic Ground State of Carbon at Temperatures Approaching 0 K

Wojciech Grochala, Angew. Chem. Int. Ed. 2014, DOI: 10.1002/anie.201400131

Highlighted by François-Xavier Coudert

Is graphite a true “ground state” of carbon not at “standard conditions” (p = 1 atm, T = 298 K) but—less arbitrarily—at p approaching 0 atm, and T approaching 0 K? And how do the thermodynamic contributions to the stability of both allotropes evolve? Here we attempt to get insight into the relative stability of graphite and diamond with the use of state-of-the-art hybrid density functional theory (DFT) methods, compare the results obtained with the comprehensive set of experimental data available, and discuss the discrepancies.

There are cases where a paper is so clearly written that it does a pretty good job of highlighting itself.  This quote above (emphasis is mine) does a pretty good job of explaining the problematic of the paper to a lay audience.

The results of the author's calculations (using HSE06/PBEsol) show that diamond actually has lower electronic energy than graphite, while the zero-point energy contribution favors graphite, bringing the two polymorphs to near-degeneracy. The vibrational contribution to entropy also favors the graphite phase, though the harmonic approximation leads to a large difference with the experimental entropy at 298 K.

The V state of ethylene: valence bond theory takes up the challenge

Wu, W.; Zhang, H.; Braïda, B.; Shaik, S.; Hiberty, P., Theor. Chem. Acc. 2014, 133, 1-13
Highlighted by Mario Barbatti

The computation of the excitation from the ground state into the first singlet ππ* state of ethylene - or the N→V transition as it is known - has been a challenge for decades.^1-4 Conventional molecular-orbital (MO) theories tend to overshoot the transition energy by far too much. A CASSCF (complete active space self-consistent field) computation in a 2-electrons/2-orbitals space with a modest basis set as the 6-31G*, for instance, predicts this transition to be 2.5 eV larger than the experimental value, 7.88 eV.

Far from being a simple curiosity restricted to ethylene, the difficulty for describing this type of state is overspread everywhere in organic photochemistry. The prediction of the Soret band in porphyrin, for example, will suffer from the same deficiencies, for the same reasons.

Two main factors contribute to the problem:

• Lack of proper electron dynamic correlation: usually, dynamic correlation is computed after the CASSCF step via perturbative or configuration interaction (CI) methods. In the case of the N→V transition, the convergence is anomalously slow. Some hardcore calculations have employed 80 million configurations in the CI expansion to obtain acceptable energies.²       
• Basis set effects: due to the ionic character of the V state, diffuse functions are essential to describe the molecular orbitals. However, the inclusion of diffuse functions also induces an artificial mixing of the V state with Rydberg states, which brings the the excitation energy closer to the experimental value by wrong reasons.

For decades, theoreticians have investigated the V state of ethylene with the most diverse methods. In 2009, Angeli showed that the dynamic response of the σ framework to the fluctuation of the π electrons is of central importance.³ It explains the reason underlying the poor convergence of the CI methods: in conventional methods, dynamic correlation is computed with a pre-optimized set of MOs, which does not include such σ-π dynamic mixing.

In this highlighted paper,⁴ Wu and co-workers systematically investigate the N→V transition using valence-bond (VB) methods. Two properties are taken into account, the transition energy and the spatial extension of the V state.With a clever sequence of calculations using different methods and levels, they showed the impact of several different factors to the predictions of the V state. 

Most impressive, they also showed that a compact set of only 5 valence bond structures (Fig. 1) is already enough to obtain a quantitatively accurate description of the N→V transition, just 0.13 eV above the experimental value. To achieve that result, however, each VB structure must have its own set of orbitals.

Fig. 1 - Set of VB structures for the computation of the N and V states in the (2,2) space. Reproduced from Ref.1.

References

(1) Bender, C. F.; Dunning Jr, T. H.; Schaefer III, H. F.; Goddard Iii, W. A.; Hunt, W. J., "Multiconfiguration wavefuntions for the lowest (ππ*) excited states of ethylene". Chem. Phys. Lett. 1972, 15, 171-178. doi: 10.1016/0009-2614(72)80143-X
(2) Müller, T.; Dallos, M.; Lischka, H., "The ethylene 1¹B_1u V state revisited". J. Chem. Phys. 1999, 110, 7176-7184. doi: 10.1063/1.478621
(3) Angeli, C., "On the Nature of the π → π* Ionic Excited States: The V State of Ethene as a Prototype". J. Comput. Chem. 2009, 30, 1319-1333. doi: 10.1002/jcc.21155
(4) Wu, W.; Zhang, H.; Braïda, B.; Shaik, S.; Hiberty, P., "The V state of ethylene: valence bond theory takes up the challenge". Theor. Chem. Acc. 2014, 133, 1-13.doi: 10.1007/s00214-013-1441-x



This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Branching Out from the Bisabolyl Cation. Unifying Mechanistic Pathways to Barbatene, Bazzanene, Chamigrene, Chamipinene, Cumacrene, Cuprenene, Dunniene, Isobazzanene, Iso-γ-bisabolene, Isochamigrene, Laurene, Microbiotene, Sesquithujene, Sesquisabinene, Thujopsene, Trichodiene, and Widdradiene Sesquiterpenes

Hong, Y. J.; Tantillo, D. J. J. Am. Chem. Soc. 2014, 136, 2450 

Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Hong and Tantillo¹ report a real tour de force computational study of multiple pathways along the routes towards synthesis of a variety of sesquiterpenes. The starting point is the bisabolyl cation 1, and a variety of rearrangements, cyclizations, proton and hydride transfers are examined to convert it into such disparate products as barbatene 2, widdradiene 3, and champinene 4. The pathways are explored at mPW1PW91/6-31+G(d,p)//B3LYP/6-31+G(d,p). Some new pathways are proposed but the main points are the sheer complexity of the C₁₅H₂₅⁺ potential energy surface and the interconnections between potential intermediates.

References

(1) Hong, Y. J.; Tantillo, D. J. "Branching Out from the Bisabolyl Cation. Unifying Mechanistic Pathways to Barbatene, Bazzanene, Chamigrene, Chamipinene, Cumacrene, Cuprenene, Dunniene, Isobazzanene, Iso-γ-bisabolene, Isochamigrene, Laurene, Microbiotene, Sesquithujene, Sesquisabinene, Thujopsene, Trichodiene, and Widdradiene Sesquiterpenes," J. Am. Chem. Soc. 2014, 136, 2450-2463, DOI:10.1021/ja4106489.

InChIs

1: InChI=1S/C15H25/c1-12(2)6-5-7-14(4)15-10-8-13(3)9-11-15/h6,8,15H,5,7,9-11H2,1-4H3/q+1
InChIKey=YKHXORRQMGBNFI-UHFFFAOYSA-N

2: InChI=1S/C15H24/c1-11-6-9-13(2)10-12(11)14(3)7-5-8-15(13,14)4/h6,12H,5,7-10H2,1-4H3/t12-,13-,14+,15-/m0/s1
InChIKey=RMKQBFUAKZOVPQ-XQLPTFJDSA-N

3: InChI=1S/C15H24/c1-12-6-7-13-14(2,3)9-5-10-15(13,4)11-8-12/h6-7H,5,8-11H2,1-4H3/t15-/m0/s1
InChIKey=SJUIWFYSWDVOEQ-HNNXBMFYSA-N

4: InChI=1S/C15H24/c1-11-6-9-15-10-12(11)14(15,4)8-5-7-13(15,2)3/h6,12H,5,7-10H2,1-4H3/t12-,14-,15-/m1/s1
InChIKey=XRDHEPAYTVHOPC-BPLDGKMQSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Protein NMR Structures Refined with Rosetta Have Higher Accuracy Relative to Corresponding X-ray Crystal Structures

Binchen Mao, Roberto Tejero, David Baker, and Gaetano T. Montelione Journal of the American Chemical Society 2014, 136, 1893

Highlighted by +Jan Jensen 

In a previous study Baker, Mentelione and co-workers showed that refining an NMR structure using Rosetta moved it closer to the x-ray structure, but increased the number of restraint violations (i.e. decreased the apparent agreement with the NMR data). A subsequent study of found the same for two additional proteins and raises intriguing questions: 

Do those violated restraints reflect true structural differences between NMR structures and X-ray crystal structures? If that is the case, then would incorporating those NMR experimental restraints into Rosetta refinement drive the NMR structure away from its X-ray counterpart?

This study sets out to answer these questions in by refining 40 NMR structures using Rosetta or Rosettta + distance and dihedral angle restraints and comparing the resulting ensembles to the corresponding x-ray structure. 

It is found that 

unrestrained Rosetta refinement generally decreases the precision of NMR structures, while restrained Rosetta refinement can increase the precision of the side chain heavy atoms of otherwise well-defined residues. Additionally, restrained Rosetta refined structures fit the unassigned NOESY peak list data significantly better than unrestrained Rosetta refined structures. Rosetta refinement can generally improve the stereochemical quality and geometry of NMR structures. More specifically, the experimental backbone dihedral angle restraints can guide Rosetta to generate models with even better backbone structures than is achieved without restraints.

Thus, it is possible to find structural ensembles that agree better with x-ray structures and the measured NMR data.  The refinement protocol allows for only relative limited movement of the protein compared to that used in protein structure determination, but converges much faster (10-20 minutes for a 100-residue protein).  So this extra step add negligible computational cost to conventional NMR protein structure determination, but probably only applicable to relatively high quality NMR structural ensembles.

Intriguingly, the relaxed X-ray structures have lower energies than the restrained-Rosetta structures for most proteins. This means that the sampling is still incomplete. But does it also point to the different between solution phase and crystal structures?  That may be so if the number of restraint violations in the relaxed X-ray structures are larger than for the restraint-refined structures. 

This work is licensed under a Creative Commons Attribution 4.0 International License.

Computational Study on the pKa Shifts in Proline Induced by Hydrogen-Bond-Donating Cocatalysts

Xue, X.-S.; Yang, C.; Li, X.; Cheng, J.-P. J. Org. Chem. 2014, 79, 1166
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Organocatalysis affected by proline is an extremely active research area, and computational chemists have made considerable contributions (see Chapter 5.3 of my book – and this is expanded on in the 2^ndedition which should be out in just a few months). Most importantly, the Houk-List model¹ for the catalysis was largely developed on the basis of computations.

Recent experiments have indicated cocatalysts that can hydrogen bond to proline may increase the catalytic effect, including the enantioselectivity. Xue and co-workers have examined a series of potential cocatalysts for their ability to enhance the acidity of proline.² This is important in that a proton transfer is a component to the key step of the Houk-List model.

The cocatalysts examined included such compounds as 1-6. The deprotonation energy of proline with the associated cocatalysts was compared with that of proline itself. The energies were computed at M06-2x/6-311++G(2df,2p)//B3LYP/6-31+G(d) with the SMD treatment of five solvents. The structure of 5with proline is shown in Figure 1.

5 with proline

5 with proline conjugate base

Figure 1. M06-2x/6-311++G(2df,2p)//B3LYP/6-31+G(d) optimized structure of 5 with proline and its conjugate base.

The effect of the cocatalysts is striking. In the gas phase, these additives decrease the pK_a of proline by 15 – 70 pK_a units, with 2 showing the largest effect. In solvent, the effect of the cocatalyst is attenuated, especially in more polar solvents, but still a considerable decrease in the pK_a is seen (as much as a 12 pK_a unit increase in acidity). Further exploration of potential cocatalysts seems fully warranted.

References

(1) Allemann, C.; Gordillo, R.; Clemente, F. R.; Cheong, P. H.-Y.; Houk, K. N. "Theory of Asymmetric Organocatalysis of Aldol and Related Reactions:  Rationalizations and Predictions," Acc. Chem. Res. 2004,37, 558-569, DOI: 10.1021/ar0300524.

(2) Xue, X.-S.; Yang, C.; Li, X.; Cheng, J.-P. "Computational Study on the pK_a Shifts in Proline Induced by Hydrogen-Bond-Donating Cocatalysts," J. Org. Chem. 2014, 79, 1166–1173, DOI: 10.1021/jo402605n.

InChIs

1: InChI=1S/CH4N2O/c2-1(3)4/h(H4,2,3,4)
InChIKey=XSQUKJJJFZCRTK-UHFFFAOYSA-N

2: InChI=1S/CH5N3/c2-1(3)4/h(H5,2,3,4)/p+1
InCiKey=ZRALSGWEFCBTJO-UHFFFAOYSA-O

3: InChI=1S/C4H4N2O2/c5-1-2(6)4(8)3(1)7/h5-6H2
InChIKey=WUACDRFRFTWMHE-UHFFFAOYSA-N

4: InChI=1S/C13H12N2S/c16-13(14-11-7-3-1-4-8-11)15-12-9-5-2-6-10-12/h1-10H,(H2,14,15,16)
InChIKey=FCSHMCFRCYZTRQ-UHFFFAOYSA-N

5: InChI=1S/C20H14O2/c21-17-11-9-13-5-1-3-7-15(13)19(17)20-16-8-4-2-6-14(16)10-12-18(20)22/h1-12,21-22H
InChIKey=PPTXVXKCQZKFBN-UHFFFAOYSA-N

6: InChI=1S/C7H13N3/c1-3-8-7-9-4-2-6-10(7)5-1/h1-6H2,(H,8,9)/p+1
InChIKey=FVKFHMNJTHKMRX-UHFFFAOYSA-O

Proline: InChI=1S/C5H9NO2/c7-5(8)4-2-1-3-6-4/h4,6H,1-3H2,(H,7,8)/t4-/m0/s1
InChIKey= ONIBWKKTOPOVIA-BYPYZUCNSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.