Kass, S. R. J. Org. Chem. 2013, 78, 7370-7372
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
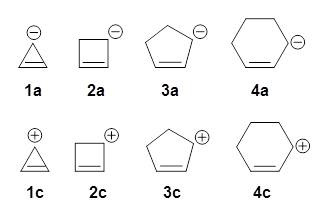

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Reposted from Computational Organic Chemistry with permission
The concept of antiaromaticity is an outgrowth of the well-entrenched notion or aromaticity. While 4n+2 π-electron systems are aromatic, 4n π-electron systems should be antiaromatic. That should mean that antiaromatic systems are unstable. The cyclopropenyl anion 1a has 4 π-electrons and should be antiaromatic. Kass has provided computational results that strongly indicate it is not antiaromatic!1
Let’s first look at the 3-cyclopropenyl cation 1c. Kass has computed (at both G3 and W1) the hydride affinity of 1c-4c. The hydride affinities of the latter three compounds plotted against the C=C-C+ angle is linear. The hydride affinity of 1c however falls way below the line, indicative of 1c being very stable – it is aromatic having just 2 π-electrons.
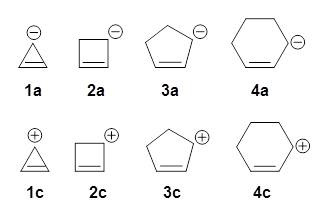
A similar plot of the deprotonation enthalpies leading to 1a-4d vs. C=C-C- angle is linear including all four compounds. If 1a where antiaromatic, one would anticipate that the deprotonation energy to form1a would be much greater than expected simply from the effect of the smaller angle. Kass suggests that this indicates that 1a is not antiaromatic, but just a regular run-of-the-mill (very) reactive anion.
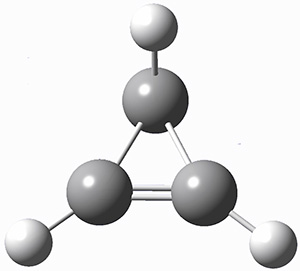
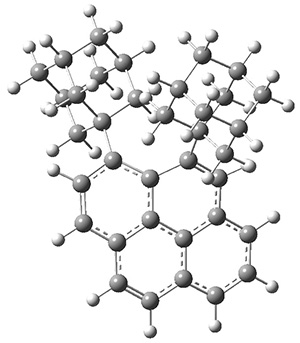
A hint at what’s going on is provided by the geometry of the lowest energy structure of 1a, shown in Figure 1. The molecule is non-planar, having Cs symmetry. A truly antiaromatic structure should be planar, really of D3h symmetry. The distortion from this symmetry reduces the antiaromatic character, in the same way that cyclobutadiene is not a perfect square and that cyclooctatraene is tub-shaped and not planar. So perhaps it is more fair to say that 1a has a distorted structure to avoid antiaromaticity, and that the idealized D3h structure, does not exist because of its antiaromatic character.
References
(1) Kass, S. R. "Cyclopropenyl Anion: An Energetically Nonaromatic Ion," J. Org. Chem. 2013, 78, 7370-7372, DOI: 10.1021/jo401350m.
InChIs
1a: InChI=1S/C3H3/c1-2-3-1/h1-3H/q-1
InChIKey=IBTMQWIWZUYLHW-UHFFFAOYSA-N
InChIKey=IBTMQWIWZUYLHW-UHFFFAOYSA-N
1c: InChI=1S/C3H3/c1-2-3-1/h1-3H/q+1
InChIKey=IPKCFGQXHZKYLH-UHFFFAOYSA-N
InChIKey=IPKCFGQXHZKYLH-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.