Discovering chemistry with an ab initio nanoreactor.

Lee-Ping Wang, Alexey Titov, Robert McGibbon, Fang Liu, Vijay S. Pande and Todd J. Martínez

Nature Chemistry

6, 1044–1048 (2014)

Contributed by Alán Aspuru-Guzik

When is quantum chemistry going to take the primary discovery role, rather than an explanatory one? This one of the questions asked in the recent Nature Chemistry paper by the groups of Vijay Pande and Todd Martínez at Stanford.

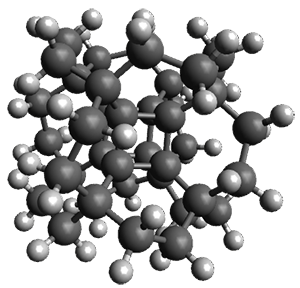
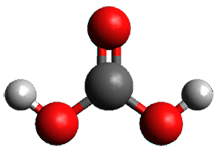
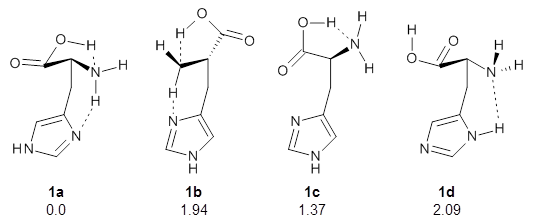
With the advent of fast GPGPU quantum chemistry in codes such as Terachem, it is practical to carry out medium-scale quantum dynamics simulations for a considerable amount of time. In this paper, the authors employ a spherical "piston" to compress and decompress high-temperature reaction mixtures, which in turn result in an accelerated process for triggering chemical reactions. Automated algorithms are employed to recognize the nature of the chemical transformations involved. The authors use this approach to identify novel mechanisms for the Urey-Miller origins of life experiment.

In this modern world of Facebook, Twitter, Youtube, Facebook and blogs, a video is worth more than a thousand words. The video below summarizes the paper very well.

This paper is indeed, one of my top 5 favorite papers in the field of computational chemistry of 2014. 

Todd Martínez explaining the future of the nanoreactor in the QUITEL 2014 conference held in the Galápagos Islands in Ecuador. He suggested, in a joking fashion, that the nanoreactor could eventually evolve a flask with molecules into life ab initio. The virtual end product of the evolution seems to be the contributor of this post.

How Electronic Dynamics with Pauli Exclusion Produces Fermi-Dirac Statistics.

Triet S. Nguyen, Ravindra Nanguneri, and John Parkhill, arxiv:14115324v1 (2014)
Contributed by Alán Aspuru-Guzik

A very interesting preprint by John Parkhill from the University of Notredame and his group provides a solution for a long-standing theoretical problem: Many of the quantum master equations that treat electron-phonon interactions fail to reach a Fermi-Dirac distribution at long times. For example, Ehrenfest dynamics is one of the usual suspects for this behavior. By employing a combination of time-dependent perturbation theory and the extended normal ordering theory of Kutzelnigg and Mukherjee, Parkhill and his co-workers arrive to a novel master equation.

The results from this work show that the Pauli principle "blocks" electron relaxation and slows it down, and in addition it leads to a time-dependent relaxation rate. The plot below shows the correct asymptotic relaxation of a double excitation in a model system and the plot in the right shows a time-dependent relaxation rate.

The paper says that "A paper using these new formulas in a useful all-electron dynamics code is

an immediate follow up.". The contributor is looking forward to it.

Computational Chemistry: 2014 in numbers

In 2014 we learnt that two of the germinal DFT papers (by Becke and Lee, Yang and Parr) are amongst the top ten most cited scientific papers of all time, and of chemistry papers published in the last ten years, the fourth and fifth most cited again relate to computational research (Truhlar and Hess, respectively). In this vein I thought it would be interesting to perform a (pseudo)-scientific analysis of the usage of computation in chemistry research in, and in the years leading up to, 2014 as judged by bibliometric data.

Searching all 2014 chemistry papers in the Web of Science for mention of "computation" or "computational" in either the article title, abstract or keywords suggests that approximately 2.7% of chemistry research involved computation of some variety this year (9,101 of a staggering 331,699 papers). This is most likely an underestimate since searching for more specific phrases such as "DFT" will turn up more hits. The same analysis over previous years reveals a steady increase in the proportion of chemistry research using computation from 0.6% in 1994, to 1.1% in 2004 and 2.2% in 2010.

Around 20% of all the computational chemistry papers published in 2014 emanate from the USA, more than double the closest competitor, China. The top ten nations in terms of publications are USA 19.5%, China 9.3%, Germany 6.1%, India 4.3%, France 4.0%, Italy 3.8%, Spain 3.7%, England 3.6%, Japan 2.7% and Canada 2.4% - making nearly 60% of the total output. A decade ago in 2004 the ten most prolific countries accounted for around 87% of total output, which indicates that recent years have witnessed a greater global involvement  in computational chemistry. Noticeable trends are seen in individual nations share of the computational chemistry pie, with the USA and some European nations effectively halving their fraction of papers between 2004 and 2014, with China's output nearly doubling from 5.4% in 2004 to 9.3% in 2014 and the emergence of India from outside the top ten into fourth place in 2014. It should be borne in mind that the globalization of science will inevitably lead to some over counting of papers here, due to multiple addresses appearing on the same paper.

Two review articles for the general audience

Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

n trying to clean up my in-box of articles for potential posts, I write here about two articles for a more general audience, authored by two of the major leaders in computational organic chemistry.

Ken Houk offers an overview of how computational simulation is a partner with experiment and theory in aiding and guiding our understanding of organic chemistry.¹ The article is written for the non-specialist, really even more for the non-scientist. Ken describes how computations have helped understand relatively simple reactions like pericyclic reactions, that then get more subtle when torquoselection is considered, to metal-catalysis, to designed protein catalysts. If you are ever faced with discussing just what you do as a computational chemist at a cocktail party, this article is a great resource of how to explain our science to the interested lay audience.

Paul Schleyer adds a tutorial on transition state aromaticity.² The authors discusses a variety of aromaticity measures (energetics, geometry, magnetic properties) that can be employed to analyze the nature of transition states, in addition to ground state molecules. This article provides a very clear description of the methods and a few examples. It is written for a more specialized audience than Houk’s article, but is nonetheless completely accessible to any chemist, even those with no computational background.

References

(1) Houk, K. N.; Liu, P. "Using Computational Chemistry to Understand & Discover Chemical Reactions,"Daedalus 2014, 143, 49-66, DOI: 10.1162/DAED_a_00305.

(2) Schleyer, P. v. R.; Wu, J. I.; Cossio, F. P.; Fernandez, I. "Aromaticity in transition structures," Chem. Soc. Rev. 2014, 43, 4909-4921, DOI: 10.1039/C4CS00012A.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Benchmarking Ab Initio Binding Energies of Hydrogen-Bonded Molecular Clusters Based on FTIR Spectroscopy

Nicolai Bork, Lin Du, Heidi Reiman, Theo Kurten, and Henrik G. Kjaergaard Journal of Physical Chemistry A 2014, 118, 5316-5322
Contributed by +Jan Jensen

One of the holy grails of computational chemistry is a method that consistently can compute standard binding free energies in bulk solvent to within 1 kcal/mol.  When using electronic structure theory one of the (many) potential problems is the use of the harmonic approximation because low-frequency modes can make a sizable contribution to the vibrational entropy. This paper provides some valuable benchmarking data.

Kjærgaard and co-workers measure the gas phase binding free energy at 295 K of acetonitrile-HCl to be between 1.2 and 1.9 kcal/mol. CCSD(T)/aug-cc-pV(T+d) predicts 2.3 kcal/mol using the harmonic frequencies and 1.9 kcal/mol using the anharmonic scaling factors suggested by Shields and co-workers.  So, at least in this case, the harmonic approximation works quite well, but can be improved quite easily using anharmonic scaling factors.  If this effect is additive and transferable, then making such a correction will be important for systems that bind using several hydrogen bonds of the 1 kcal/mol accuracy-target is to be met.

The authors write "We find that this energy lowering originates almost entirely from the scaling of the two lowest frequency modes (between 28 and 35 cm$^{-1}$, depending on method), emphasizing the importance of calculating the low frequency modes accurately."

Indeed, such low frequency modes are susceptible to numerical noise (e.g. from coarse DFT grids or sloppy optimization convergence criteria) which can even lead to them turning up as imaginary frequencies in the vibrational analysis. Because imaginary frequencies are not included in the vibrational free energy, this can lead to sizable errors in the binding free energy.  For example, a 28 cm$^{-1}$ frequency contributes 1.8 kcal/mol to the free energy at 295 K.

B3LYP-D3, MP2 and PW91/aug-cc-pV(T+d) calculations also yield binding free energies within the experimentally measured range, but in the last two cases this is due for fortunate cancellation of errors in the electronic and free energy components based on comparison to the CCSD(T) calculations.  Having said that, with the exception of B3LYP, all functionals tested in this study are able to predict the binding energy to within 1 kcal/mol using the aug-cc-pV(T+d) basis set.

It is worth noting that the approach by Shields and co-workers find scaling factors by fitting to harmonic vibrational energy and entropy-expressions evaluated using anharmonic fundamental frequencies.  It is not at all obvious (at least to me) that this approach will result in good agreement with experimental binding free energies involving 28 cm$^{-1}$ frequencies, so this (and a previous) study provides very valuable validation of this general approach.



This work is licensed under a Creative Commons Attribution 4.0 International License.

Hypercubane: DFT-based prediction of an Oh-symmetric double-shell hydrocarbon

Pichierri, F. Chem. Phys. Lett. 2014, 612, 198-202
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Three-dimensional objects can be projected into four-dimensional objects. So for example a cube can be projected into a hypercube, as in Scheme 1.

Scheme 1.

Pichierri proposes a hydrocarbon analogue of the hypercube. The critical decision is the connecting bridge between the outer (exploded) carbons. This distance is too long to be a single carbon-carbon bond. Pichierri opts to use ethynyl bridges, to give the hypercube 1.¹

Now, unfortunately he does not supply any supporting materials. So I have reoptimized this O_h geometry at B3LYP/6-31G(d), and show this structure in Figure 1. Pichierri does not report much beyond the geometry of 1 and the perfluoronated analogue. One interesting property that might be of interest is the ring strain energy of 1, which I will not take up here.

1

2

But a question I will take up is just what bridges might serve to create the hydrocarbon hypercube. A more fundamental choice might be ethanyl bridges, to create 2. However, the O_h conformer of 2 has 13 imaginary frequencies at B3LYP/6-31G(d). Lowering the symmetry to D₃ give a structure that has only real frequencies, and it’s shown in Figure 1. An interesting exercise is to ponder other choices of bridges, which I will leave for the reader.

1

2

Figure 1. B3LYP/6-31G(d) optimized structures of 1 and 2.
As always, be sure to click on the image to enable Jmol for interactive viewing of these interesting structures!

References

(1) Pichierri, F. "Hypercubane: DFT-based prediction of an O_h-symmetric double-shell hydrocarbon,"Chem. Phys. Lett. 2014, 612, 198-202, DOI: j.cplett.2014.08.032.

InChIs

1: InChI=1S/C40H24/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H
InChIKey=FFMFUIDOGFAUOP-UHFFFAOYSA-N

2: InChI=1S/C40H48/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H2
InChIKey=MCSZKKKJCDSRIV-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Benchmarks for Characterization of Minima, Transition States, and Pathways in Atomic, Molecular, and Condensed Matter Systems

Samuel T. Chill, Jacob Stevenson, Victor Ruehle, Cheng Shang, Penghao Xiao, James D. Farrell, David J. Wales, and Graeme Henkelman Journal of Chemical Theory and Computation 2014 10, 5476–5482
Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission

One of the key tasks that atomistic simulations of all types perform is to characterise a potential energy surface.  This includes diverse problems, such as:

• local optimisation (finding a stable structure given a starting set of coordinates)
• global optimisation (finding the most stable structure for a given set of atoms – a very hard task !)
• transition state searches, both starting from one minimum (single-ended) and interpolating between two minima (double-ended)

These are hugely complex problems, and there are many methods which have been proposed to perform these searches. I have discussed some of these before (here, here,  and here); there is also an overview of searching methods in Chapter 5 of the book.

The paper I’m discussing in this post[1] proposes some benchmarks to test different methods for these optimisation problems.  They also offer a website[2] where the tests can be found, and new results shared.  The problems are all based around simple empirical potentials (which makes the testing relatively light).  They propose the following systems:

• a 38 atom Lennard-Jones cluster
• a 100 atom, two species Lennard-Jones cluster
• water clusters with 10, 15 and 20 atoms modelled with TIP4P
• a seven atom cluster on the (111) surface of a FCC material (Morse potential)
• a bulk sample of the same FCC material

These different problems cover a reasonable set of problems, but there is no reason why more should not be added to the set.  For instance, the present set lacks any examples of covalent bond-breaking systems.

Various methods are compared, including L-BFGS, FIRE and conjugate gradients, nudged elastic band, eigenvector following and basin hopping.  There are so many methods that it would be impossible to cover all, but I’m a little surprised that methods such as AIRSS and metadynamics weren’t tested for the global optimisation problems.

The local optimisation problem offers the simplest problem to characterise, and the conclusions are simplest here: methods that include curvature (L-BFGS and conjugate gradients) are significantly faster.  This is not particularly surprising, as these methods are known to be well optimised, and the test suite avoids any pathological problems.  The conclusions for the other challenges are less clear; the global optimisation problem in particular seems not to distinguish well between the two methods used.

The saddle point searching results surprised me.  I use the nudged-elastic band (NEB) method regularly, and one of the authors is a leading figure in the development of the method, but it did not perform particularly well.  The study did show that the performance is dependent on the initial pathway guessed, and suggested that for double-ended searches an preliminary NEB search should then be refined by the eigenvector following method.  The eigenvector following method performed best on the single-ended searches as well.

What do we learn from the paper ? While the overall conclusions confirm expectations for local optimisation and do not discriminate as much as would be hoped for the other problems, it’s an excellent start.  In particular, in seeking to offer open, standard tests for all the different methods that are available, it offers a way to move forward in this field.  It also suggests an excellent new model of characterisation-based scientific papers: a dynamic database of freely-available results.

[1] J. Chem. Theor. Comput. 10, 5476 (2014) DOI: 10.1021/ct5008718

[2] http://optbench.org/

Gas-Phase Preparation of Carbonic Acid and Its Monomethyl Ester

Reisenauer, H. P.; Wagner, J. P.; Schreiner, P. R.  Angew. Chem. Int. Ed. 2014, 53, 11766-11771
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

I remain amazed at how regularly I read reports of structure determinations of what seem to be simple molecules, yet these structures have eluded determination for decades if not centuries. An example is the recently determined x-ray crystal structure of L-phenylalanine;¹ who knew that growing these crystals would be so difficult?

The paper I want to discuss here is on the gas-phase structure of carbonic acid 1.² Who would have thought that preparing a pure gas-phase sample would be so difficult? Schreiner and co-workers prepared carbonic acid by high-vacuum flash pyrolysis (HVFP) of di-tert-butyl carbonate, as shown in Scheme 1.

Scheme 1

Carbonic acid can appear in three difference conformations, shown in Figure 1. The two lowest energy conformations are separated by a barrier of 9.5 kcal mol^-1 (estimated by focal point energy analysis). These conformations can be interconverted using near IR light. The third conformation is energetically inaccessible.

1cc (0.0)	1ct (1.6)	1tt (10.1)
2cc		2cc

Figure 1. CCSD(T)/cc-pVQZ optimized structures of 1 (and the focal point relative energies in kcal mol^-1) and the CCSD(T)/cc-pVTZ optimized structures of 2.

The structures of these two lowest energy conformations were confirmed by comparing their experimental IR spectra with the computed spectra (CCSD(T)/cc-pVTZ) and their experimental and computed rotational constants.

An interesting added component of this paper is that sublimation of the α- and β-polymorphs of carbonic acid do not produce the same compound. Sublimation of the β-isomorph does produce 1, but sublimation of the α-isomorph produces the methylester of 1, compound 2 (see Figure 1). The structure of 2 is again confirmed by comparison of the experimental and computed IR spectra.

References

(1) Ihlefeldt, F. S.; Pettersen, F. B.; von Bonin, A.; Zawadzka, M.; Görbitz, C. H. "The Polymorphs of L-Phenylalanine," Angew. Chem. Int. Ed. 2014, 53, 13600–13604, DOI: 10.1002/anie.201406886.

(2) Reisenauer, H. P.; Wagner, J. P.; Schreiner, P. R. "Gas-Phase Preparation of Carbonic Acid and Its Monomethyl Ester," Angew. Chem. Int. Ed. 2014, 53, 11766-11771, DOI: 10.1002/anie.201406969.

InChIs

1: InChI=1S/CH2O3/c2-1(3)4/h(H2,2,3,4)
InChIKey=BVKZGUZCCUSVTD-UHFFFAOYSA-N

2: InChI=1S/C2H4O3/c1-5-2(3)4/h1H3,(H,3,4)
InChIKey=CXHHBNMLPJOKQD-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Tautomerism in Neutral Histidine

Bermúdez, C.; Mata, S.; Cabezas, C.; Alonso, J. L. Angew. Chem. Int. Ed. 2014, 53, 11015-11018
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

The Alonso group has yet again (see these posts) determined the gas-phase structure of an important, biologically significant molecule using a combination of exquisite microwave spectroscopy and quantum computations. This time they examine the structure of histidine.¹

They optimized four conformations of histidine, as its neutral tautomer, at MP2/6-311++G(d,p). These are schematically drawn in Figure 1. Conformer 1a is the lowest in free energy, likely due to the two internal hydrogen bonds. Its structure is shown in Figure 2.

Figure 1. The four conformers of histidine. The relative free energy (MP2/6-311++G(d,p)) in kcal mol^-1are also indicated.

Figure 2. MP2/6-311++G(d,p) optimized geometry of 1a.

The initial experimental rotation constants were only able to eliminate 1b from consideration. So they then determined the quadrupole coupling constants for the ¹⁴N nuclei. These values strongly implicated 1a as the only structure in the gas phase. The agreement between the experimental values and the computed values at MP2/6-311++G(d,p) was a concern, so they rotated the amine group to try to match the experimental values. This lead to a change in the NHCC dihedral value of -16° to -23° Reoptimization of the structure at MP2/cc-pVTZ led to a dihedral of -21° and overall excellent agreement between the experimental spectral parameters and the computed values.

It is somewhat disappointing the supporting materials does not include the structures of the other three isomers, nor the optimized geometry at MP2/cc-pVTZ.

References

1) Bermúdez, C.; Mata, S.; Cabezas, C.; Alonso, J. L. "Tautomerism in Neutral Histidine," Angew. Chem. Int. Ed. 2014, 53, 11015-11018, DOI: 10.1002/anie.201405347.

InChIs

Histidine: InChI=1S/C6H9N3O2/c7-5(6(10)11)1-4-2-8-3-9-4/h2-3,5H,1,7H2,(H,8,9)(H,10,11)/t5-/m0/s1
InChIKey=HNDVDQJCIGZPNO-YFKPBYRVSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Quantum Chemical Approach to Estimating the Thermodynamics of Metabolic Reactions

Adrian Jinich, Dmitrij Rappoport, Ian Dunn, Benjamin Sanchez-Lengeling, Roberto Olivares-Amaya, Elad Noor, Arren Bar Even & Alán Aspuru-Guzik Sci. Rep. 2014, 4, 7022

Contributed by +Jan Jensen 

'

DOI: 10.1038/srep07022 CC-BY-NC-ND

Computational chemistry is finally in a position to conduct studies on hundreds or even thousands of molecules within a reasonable amount of time.  This has led to benchmark datasets which have been used to develop new semi-empirical methods (e.g. DFT-Dx or HF-3c) as well as high-throughput screening of molecules with desirable properties. 

This paper represents a third kind of study: a concerted effort to fill in missing experimental data needed to quantitatively understand a complex chemical system - in this case cellular metabolism. Standard Gibbs reaction free energies of biochemical reactions are crucial to quantitative modeling of metabolism (metabolic flux analysis) but only a small fraction have been measured experimentally.  

Many of the reactions involve molecule-sizes that can be modeled routinely by electronic structure calculations.  However, there are new challenges compared to, for example, atmospheric chemistry such as the modeling of pH- and solvation-effects and multiply charged ions.  Thus, any conformational search must often be repeated for several different protonation states and multiply charged ions often necessitate the treatment of explicit solvent molecules and, even then, result in relatively solvation energies with relatively large errors.  Also, multiply charged anions may present additional problems for DFT due to incomplete cancellation of the inter-electronic Coulomb repulsion at larger distances. 

This paper represents the first, pioneering, attempt to address these issues with high-throughput in mind and the results are encouraging. For reactions involving non-multiply charged species B3LYP/6-31G* with the COSMO solvation model augmented by explicit water molecules result in MADs less than 5 kcal/mol, while being fast enough to compute more than a hundred reaction energies (involving more than 5000 quantum calculations). 

However, this paper is more a call to action than the definitive answer.  Many new methodological improvements (perhaps such as this one?) are needed in order to increase the accuracy and efficiency needed produce a complete and accurate picture of cellular metabolism. I hope this paper will spur such developments - hopefully in the form of large and open collaborations (perhaps similar to this one?).  

Thanks to Adrian Jinich for alerting me to this paper

This work is licensed under a Creative Commons Attribution 4.0 International License.

Isotope Effects, Dynamic Matching, and Solvent Dynamics in a Wittig Reaction. Betaines as Bypassed Intermediates

Chen, Z.; Nieves-Quinones, Y.; Waas, J. R.; Singleton, D. A.  J. Am. Chem. Soc. 2014, 136, 13122-13125
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

If you hadn’t noticed, I am a big fan of the work that Dan Singleton is doing concerning the role of dynamics in discerning reaction mechanisms. Dan’s group has reported another outstanding study combining experiments, traditional QM computations, and molecular dynamics – this time on the Wittig reaction.¹

The key question concerning the mechanism is whether a betaine intermediate is accessed along the reaction (path A) or whether the reaction proceeds in a concerted manner (path B). Earlier computations had supported the concerted pathway (B).

Experimental determination of the heavy atom kinetic isotope effect was made for Reaction 1.

Reaction 1

Using the 6-31+G(2df,p) basis set, three different density functionals predict three different potential energy surfaces. With M06-2x, the surface indicates path A (stepwise), with the first step rate-limiting. B3P86 also predicts the stepwise reaction, but the second step is rate-limiting. The Lc-wPBE functional predicts a concerted reaction. Using these surfaces, they predicted the carbon isotope effect and compared it to the experimental values. The best agreement is with the M06-2x surface with a weighting of the vibrational energies of the two different TSs. The optimized structures of the two transition states, the betaine intermediate, and the product are shown in Figure 1.

TS1	Betaine
TS2	Product

Figure 1. M06-2x/6-31+G(2df,p) optimized geometry of the critical points of Reaction 1.

The agreement of the predicted and experimental KIE is not ideal. So, they performed molecular dynamics computations with the ONIOM approach using M06-2x/6-31G* for Reaction 1 and 53 THF molecules treated at PM3. 360 trajectories were begun in the region of the first transition state (TS1), and they can be organized into 4 groups. The first group (128 trajectories) are reactions that produce product. The second group (76 cases) form the C-C bond but then it ruptures and returns to reactant. The third group (82 cases) have an immediate recrossing back to reactant, and the last group (16 cases) takes product back to the first TS and then returns to product. The predicted KIE using this weighted MD results gives values in outstanding agreement with the experiments.

Of the first group, about 50% pass from TS1 to TS2 in less than 150 fs, or in other words look like a concerted path. But a good number of trajectories reside in the betaine region for 1-2 ps.

In contrast, trajectories initiated from the betaine with equilibrated THF molecules indicate a median of 600 ps to travel from TS1 to TS2 and do not resemble a concerted path.

They argue that this bimodal distribution is in part associated with a solvent effect. When the first TS is crossed the solvent molecules are not equilibrated about the solute, and 10-20% of the trajectories immediately pass through the betaine region due to “dynamic matching” where the entering motion matches with exiting over the second transition state. The longer trajectories result from improper dynamic matching, but faster motion in the solute than motion amongst the solvent needed to stabilize the betaine. So, not only do we need to be concerned about dynamic effects involving the reactants, we need to be concerned about dynamics associated with the solvent too!

References

(1) Chen, Z.; Nieves-Quinones, Y.; Waas, J. R.; Singleton, D. A. "Isotope Effects, Dynamic Matching, and Solvent Dynamics in a Wittig Reaction. Betaines as Bypassed Intermediates," J. Am. Chem. Soc. 2014, 136, 13122-13125, DOI: 10.1021/ja506497b.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Energy-conserving ab initio molecular dynamics

Contributed by David Bowler
Reposted from Atomistic Computer Simulations with permission

Energy conservation in molecular dynamics is an important test of the propagators and parameters being used.  In first principles Born-Oppenheimer molecular dynamics (BOMD) this is complicated because of the need for self-consistent iteration to a consistent ground state charge density and potential.  The self-consistency cycle introduces errors since it is not possible to achieve a perfect ground state.  Moreover, to improve efficiency, the starting charge density is often predicted from previous charge densities; while this can results in impressive speed gains, it breaks the time-reversibility of the dynamics and will introduce an unavoidable energy drift.

This blog will discuss a set of papers[1-4] from Anders Niklasson in Los Alamos, which seek to remove this problem, and which have also shown a way to avoid the self-consistency cycle entirely.  The work is perhaps less well-known that it should be, and offers an excellent route to efficiency.  The recent linear scaling DFT molecular dynamics that we have published (going to over 32,000 atoms with DFT)[5] used the time-reversible formulation to conserve energy.

The time reversibility is built on an extended Lagrangian (and is known as XL-BOMD) which introduces a new dynamical variable, or set of variables, for the electronic degrees of freedom (whether charge density or density matrix) alongside the nuclear degrees of freedom, in a trick reminiscent of Car-Parrinello MD[6].  This degree of freedom, written below as P, evolves harmonically in time, depending on a frequency (set by the user) and the difference to the ground state charge density (or whatever is being used).

This degree of freedom, P, can be propagated in a time-reversible manner with an accuracy that only depends on the timestep.  The BOMD can thus be made time-reversible by starting the self-consistency cycle from P – resulting in stability and energy conservation in MD over long timescales.  On its own, this is a very valuable advance.

However, in a set of papers[2-4], Niklasson takes the idea further.  He suggests that, given the right functional for the energy, the self-consistency cycle can be removed.  This involves performing a single diagonalisation/minimisation without self-consistent update, and using P as the input charge density.  The scheme has been developed, with the latest paper[4] generalising the earlier work, and showing that the approach is applicable to systems regardless of gap, provided that an adiabatic separation between electronic and nuclear degrees of freedom can be made.

This work provides techniques to accelerate ab initio MD significantly; we have found that, in combination with linear scaling DFT, we can access picoseconds of MD for tens of thousands of atoms even with a simple initial implementation.  The two approaches together promise to make large-scale, long time accurate MD significantly more affordable.

[1] Phys. Rev. Lett. 100, 123004 (2008) DOI:10.1103/PhysRevLett.100.123004

[2] J. Chem. Phys. 139, 214102 (2013) DOI:10.1063/1.4834015

[3] J. Chem. Phys. 140, 044117 (2014) DOI:10.1063/1.4862907

[4] J. Chem. Phys. 140, 164123 (2014) DOI:10.1063/1.4898803

[5] arxiv 1409.6085 and J. Chem. Theor. Comput. in press (2014) DOI:10.1021/ct500847y

Solution-Phase Dimerization of an Oblong Shape-Persistent Macrocycle

Chu, M.; Scioneaux, A. N.; Hartley, C. S.  J. Org. Chem. 2014, 79, 9009–9017
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

π-π-stacking has been a major theme of my blog, and is discussed in Chapter 3.5.4 in the Second Edition of my book. Most examples involved molecules that are nearly circular (like benzene or triphenylene). Hartley and co-workers discuss the π-π-stacking of the oblong molecule 1, comparing its experimental features with computed features of the model compound 2.¹

The key spectroscopic feature associated with assembly of 1 are the changes in the ¹H chemical shifts with increasing concentration. For example, the chemical shift of the three protons on the triphenylene unit shift upfield by 0.30 to 0.66 ppm as the concentration increases from 10^-5 to 10^-2 M.

To see if these NMR shift changes are due to association of 1, they employed a computational approach. First they optimized the structure of model compound 2 at B3LYP/6-31G(d) (Shown in Figure 1a). Then using this fixed geometry, they computed the ¹H chemical shifts of the dimer of 2. They explored the stacking distance (ranging from 3.2 to 4.0 Å along with varying the displacement of the two molecules along the major axis from 0.0 to 6.0 Å, finding the best fit to the chemical shifts with a separation of 3.6 Å and a displacement along the major axis of 3.5 Å. Using these two fixed values, they explored displacement of the molecules along the minor axis, along with rotation of the two molecules. The best fit to the experimental chemical shifts was with a displacement of 0.5 Å along the short axis and no rotation. This structure is shown in Figure 1b, with a RMS error of only 0.09 ppm from experiment. Models of the trimer show poorer fit to the experimental data.

(a) 2

(b) 2 dimer

Figure 1. B3LYP/6-31G(d) (a) optimized structure of 2 and the (b) structure of the best fit of the dimer of2. (As always, clicking on these images will allow you to manipulate the 3-D structure using JMol – highly recommended for the dimer.)

Using some smaller models and the B97-D functional, they argue that the displacement, which is substantially larger than the displacement found in stacked triphenylene, results from the need to minimize the steric interactions between the alkoxyl chains.

References

(1) Chu, M.; Scioneaux, A. N.; Hartley, C. S. "Solution-Phase Dimerization of an Oblong Shape-Persistent Macrocycle," J. Org. Chem. 2014, 79, 9009–9017; DOI: 10.1021/jo501260c.

InChIs:

1: InChI=1S/C116H148O10/c1-11-21-31-41-59-117-95-71-87-51-55-91-75-97-99(103-81-111(121-63-45-35-25-15-5)115(125-67-49-39-29-19-9)85-107(103)105-83-113(123-65-47-37-27-17-7)109(79-101(97)105)119-61-43-33-23-13-3)77-93(91)57-53-89-70-90(74-96(73-89)118-60-42-32-22-12-2)54-58-94-78-100-98(76-92(94)56-52-88(69-87)72-95)102-80-110(120-62-44-34-24-14-4)114(124-66-48-38-28-18-8)84-106(102)108-86-116(126-68-50-40-30-20-10)112(82-104(100)108)122-64-46-36-26-16-6/h69-86H,11-50,59-68H2,1-10H3
InChIKey=UUKOQEVXPHHWBJ-UHFFFAOYSA-N

2: InChI=1S/C76H68O10/c1-11-77-55-31-47-21-25-51-35-57-59(63-41-71(81-15-5)75(85-19-9)45-67(63)65-43-73(83-17-7)69(79-13-3)39-61(57)65)37-53(51)27-23-49-30-50(34-56(33-49)78-12-2)24-28-54-38-60-58(36-52(54)26-22-48(29-47)32-55)62-40-70(80-14-4)74(84-18-8)44-66(62)68-46-76(86-20-10)72(82-16-6)42-64(60)68/h29-46H,11-20H2,1-10H3
InChIKey=NGTKTKCZPONPTB-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.