Alonso, J. L.; Vaquero, V.; Peña, I.; López, J. C.; Mata, S.; Caminati, W. Angew. Chem. Int. Ed. 2013, 52, 2331-2334
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission
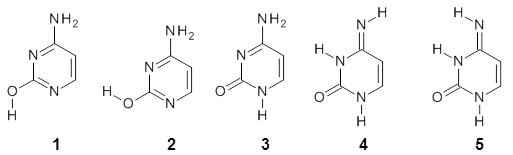
Alonso and coworkers have again (see this post employed laser-ablation molecular-beam Fourier-transform microwave (LA-MB-MW)spectroscopy to discern the gas phase structure of an important biological compound: cytosine.1 They identified five tautomers of cytosine 1-5. Comparison between the experimental and computational (MP2/6-311++G(d,p) microwave rotational constants and nitrogen nuclear quadrupole coupling constants led to the complete assignment of the spectra. The experimental and calculated rotational constants are listed in Table 1.

Table 1. Rotational constants (MHz) for 1-5.
1
|
2
|
3
|
4
|
5
| ||||||
Expt
|
calc
|
Expt
|
calc
|
Expt
|
calc
|
Expt
|
calc
|
Expt
|
calc
| |
A
|
3951.85
|
3934.5
|
3889.46
|
3876.5
|
3871.55
|
3856.0
|
3848.18
|
3820.1
|
3861.30
|
3844.2
|
B
|
2008.96
|
1999.1
|
2026.32
|
2014.7
|
2024.98
|
2012.3
|
2026.31
|
2019.0
|
2011.41
|
1999.7
|
C
|
1332.47
|
1326.8
|
1332.87
|
1326.9
|
1330.34
|
1323.3
|
1327.99
|
1324.0
|
1323.20
|
1318.4
|
The experimental and computed relative free energies are listed in Table 2. There is both not a complete match of the relative energetic ordering of the tautomers, nor is there good agreement in their magnitude. Previous computations2 at CCSD(T)/cc-pVQZ//CCSD//cc-pVTZ are in somewhat better agreement with the gas-phase experiments.
Table 2. Relative free energies (kcal mol-1) of 1-5.
expt
|
MP2/
6-311++G(d,p) |
CCSD(T)/cc-pVQZ//
CCSD//cc-pVTZ | |
1
|
0.0
|
0.0
|
0.0
|
2
|
0.47
|
0.70
|
0.7
|
3
|
0.11
|
1.19
|
0.2
|
4
|
0.83
|
3.61
|
0.7
|
5
|
5.22
|
References
(1) Alonso, J. L.; Vaquero, V.; Peña, I.; López, J. C.; Mata, S.; Caminati, W. "All Five Forms of Cytosine Revealed in the Gas Phase," Angew. Chem. Int. Ed. 2013, 52, 2331-2334, DOI:10.1002/anie.201207744.
(2) Bazso, G.; Tarczay, G.; Fogarasi, G.; Szalay, P. G. "Tautomers of cytosine and their excited electronic states: a matrix isolation spectroscopic and quantum chemical study," Phys. Chem. Chem. Phys., 2011,13, 6799-6807, DOI:10.1039/C0CP02354J.
InChIs
cytosine: InChI=1S/C4H5N3O/c5-3-1-2-6-4(8)7-3/h1-2H,(H3,5,6,7,8)
InChIKey=OPTASPLRGRRNAP-UHFFFAOYSA-N
InChIKey=OPTASPLRGRRNAP-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.