Assessing the Accuracy of Density Functional and Semiempirical Wave Function Methods for Water Nanoparticles: Comparing Binding and Relative Energies of (H2O)16 and (H2O)17 to CCSD(T) Results

Leverentz, H. R.; Qi, H. W.; Truhlar, D. G. J. Chem. Theor. Comput. 2013, ASAP
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

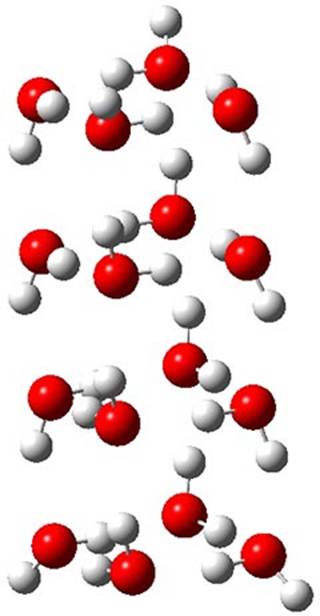
Truhlar has made a comparison of binding energies and relative energies of five (H₂O)₁₆ clusters.¹ While technically not organic chemistry, this paper is of interest to the readership of this blog as it compares a very large collection of density functionals on a problem that involves extensive hydrogen bonding, a problem of interest to computational organic chemists.

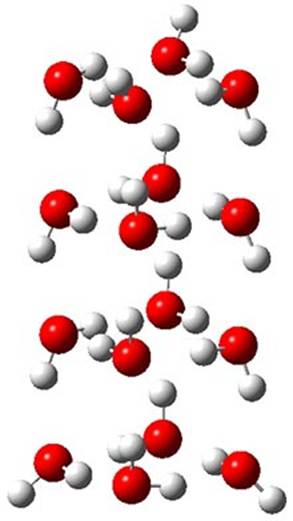
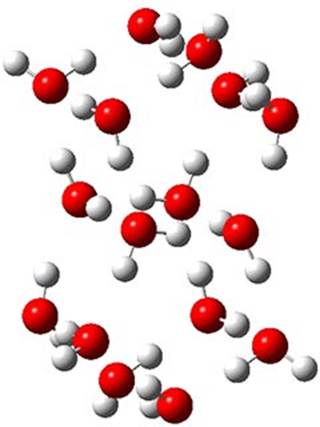
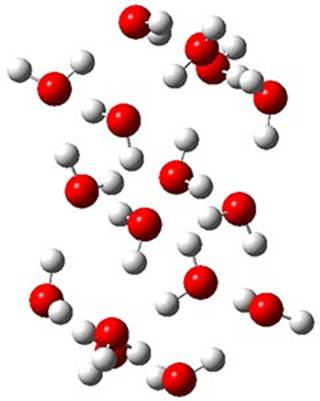
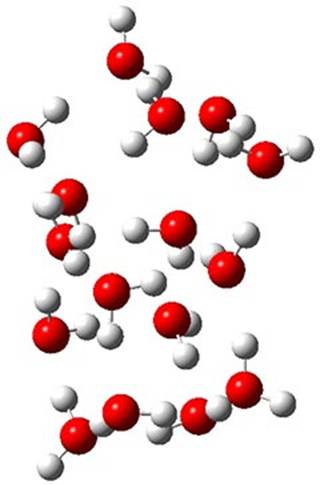
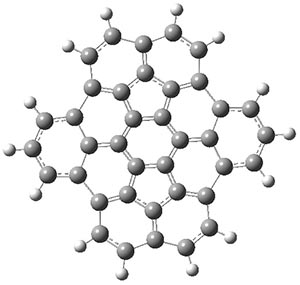
The CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ energies of clusters 1-5 (shown in Figure 1) were obtained by Yoo.² These clusters are notable not just for their size but also that they involve multiple water molecules involved in four hydrogen bonds. Truhlar has used these geometries to compute the energies using 73 different density functionals with the jun-cc-pVTZ basis set (see this post for a definition of the ‘jun’ basis sets). Binding energies (relative to 16 isolated water molecules) were computed along with the 10 relative energies amongst the 5 different clusters. Combining the results of both types of energies, Truhlar finds that the best overall performance relative to CCSD(T) is obtained with ωB97X-D, a hybrid GGA method with a dispersion correction. The next two best performing functionals are LC-ωPBE-D3 and M05-2x. The best non-hybrid performance is with revPBE-D3 and B97-D.

1 (0.0)	2 (0.25)
3 (0.42)	4 (0.51)
5 (0.54)

Figure 1. MP2/aug-cc-pVTZ optimized geometries and relative CCSD(T) energies (kcal mol^-1) of (water)₁₆ clusters 1-5. (Don’t forget to click on any of these molecules above to launch Jmol to interactively view the 3-D structure. This feature is true for all molecular structures displayed in all of my blog posts.)

While this study can help guide selection of a functional, two words of caution. First, Truhlar notes that the best performing methods for the five (H₂O)₁₆ clusters do not do a particularly great job in getting the binding and relative energies of water hexamers, suggesting that no single functional really stands out as best. Second, a better study would also involve geometry optimization using that particular functional. Since this was not done, one can garner little here about what method might be best for use in a typical study where a geometry optimization must also be carried out.

References

(1) Leverentz, H. R.; Qi, H. W.; Truhlar, D. G. "Assessing the Accuracy of Density
Functional and Semiempirical Wave Function Methods for Water Nanoparticles: Comparing Binding and Relative Energies of (H₂O)₁₆ and (H₂O)₁₇ to CCSD(T) Results," J. Chem. Theor. Comput. 2013, ASAP, DOI:10.1021/ct300848z.

(2) Yoo, S.; Aprà, E.; Zeng, X. C.; Xantheas, S. S. "High-Level Ab Initio Electronic Structure Calculations of Water Clusters (H₂O)₁₆ and (H₂O)₁₇: A New Global Minimum for (H₂O)₁₆," J. Phys. Chem. Lett. 2010, 1, 3122-3127, DOI: 10.1021/jz101245s.

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

Using Orbital Symmetry to Minimize Charge Recombination in Dye-Sensitized Solar Cells

Maggio, E., Martsinovich, N. and Troisi, A. (2013), Angew. Chem. Int. Ed., 52: 973–975.
Contributed by Gemma Solomon 

Orbital symmetry can be used in dye design to retard charge recombination in dye-sensitized solar cells. 

Copyright © 2013 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

Finding the balance between competing processes is a central challenge in optimizing the performance of dye-sensitized solar cells. One aspect of this problem is the dichotomy between the requirement for fast charge injection between the dye and a semiconductor surface (for photo-induced charge separation) and slow charge recombination between the two. There are a range of strategies available for optimizing one or other of these processes; but clever chemical design is required in order to optimize the two together. Minimizing unwanted charge recombination involves beating the Coulomb interaction, and this is a formidable opponent indeed.

In their recent paper Maggio, Martsinovich and Troisi have proposed an elegant solution: use orbital symmetry to retard charge recombination. Building on the ideas from studies of electron transfer, they show that it is possible to design dyes where the charge injection is symmetry allowed, while charge recombination is symmetry forbidden. In terms of molecular orbitals, charge recombination involves injection into the HOMO of the dye from the semiconductor, while charge injection involves the LUMO of the dye injecting into the surface. Depending on the symmetry of the dye, and the position at which it is substituted, the authors show that it is possible to have the LUMO interacting strongly with the surface (delocalizing into the binding arm) while the HOMO remains isolated, as illustrated above.

This represents a new strategy for dye design and an exciting prediction from computational chemistry. It will be interesting to see how dyes using this strategy perform in devices and should remind us all that we have a powerful tool for molecular design with symmetry at our disposal.   

Supramolecular Binding Thermodynamics by Dispersion-Corrected Density Functional Theory

Stefan Grimme Chemistry A European Journal 2012, 18, 9955 (Paywall)
Contributed by +Jan Jensen

Computing accurate binding free energies is a fundamental challenge to molecular modeling.  I recently highlighted a study by +Hari Muddana and +Michael Gilson where the binding free energies of 29 ligands to the host CB7 were reproduced with an RMSE of 1.9 kcal/mol using  PM6-DH+, though this involved fitting of the solvation free energy change.

In this study Grimme presents a computational methodology that reproduces binding free energies of 13 chemically diverse host-guest complexes with a MAD of 2.1 kcal/mol.  Though the accuracies of the two studies are similar there are many differences between the two approaches.

The gas phase interaction energies are computed using dispersion corrected DFT calculations.  Practically, this means that, unlike the study by Muddana and Gilson, no conformational averaging is performed.  The dispersion correction includes a three-body term that is shown to contribute up to 4.6 kcal/mol to the gas phase interaction energy.  The similar three-body terms also contribute to the vibrational free energy contributions (see below) and together with the gas phase contributions lower the MAD by 1.3 kcal/mol compared to experimental binding free energies.

Similarly, the solvation free energy is computed using DFT and COSMO and, unlike the Muddana and Gilson paper, is not corrected empirically.  This may be due to the fact that the DFT/COSMO calculations (including the radii used to define the surface) already has been carefully calibrated while the PM6/COSMO calculations have not.

The vibrational free energy corrections are computed in the gas phase using dispersion and hydrogen-bond corrected PM6 and DFTB (PM6-D3H and DFTB-D3H, respectively).  These corrections were developed as part of this study based on the S66 data set and implemented in an external program interfaced with the MOPAC and DFTB codes (Grimme, personal communications).

The vibrational entropy contribution increases exponentially with decreasing vibrational frequency and this can introduce numerical unstable binding free energies for these systems as low vibrational frequencies are common.  Grimme deals with this problem by introducing a hybrid function where the vibrational entropy is smoothly replaced (using a switching function) with a corresponding free-rotor entropy for low frequency modes.  As computed in his study, the free-rotor entropy increases much less steeply as the vibrational frequency decreases and produced binding free energies that are in better agreement with experiment. However, computing numerically stable vibrational frequencies for low frequency modes remains a challenge for these systems and may require manual intervention (Grimme, personal communications).  

Thanks to +Hari Muddana for alerting me to this paper and to Stefan Grimme for personal communications.

 
This work is licensed under a Creative Commons Attribution 3.0 Unported License. 

Bowl-Shaped Fragments of C70 or Higher Fullerenes: Synthesis, Structural Analysis, and Inversion Dynamics

Wu, T.-C.; Chen, M.-K.; Lee, Y.-W.; Kuo, M.-Y.; Wu, Y.-T. Angew. Chem. Int. Ed. 2013, 52, 1289-1293
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

I have discussed a few bowl-shaped aromatics in this blog (see for example this and this). Kuo and Wu now report on a few bowls derived from C₇₀-fullerenes.¹ The bowl 1 was synthesized (along with a couple of other derivatives) and its x-ray structure obtained. As anticipated this polyclic aromatic is not planar, but rather a definite bowl, with a bowl depth of 2.28 Å. This is less curved than when the fragment is present in C₇₀-fullerene.

1

Interestingly, this bowl does not invert through a planar transition state. The fully planar structure 1pl, shown in Figure 1, is 116 kcal mol^-1 above the ground state bowl structure, computed at B3LYP/cc-pVDZ. Rather, the molecule inverts through a twisted S-shaped structure 1TS, also shown in Figure 1. The activation barrier through 1TS is 80 kcal mol^-1. This suggests that 1 is static at room temperature, unlike corranulene which has an inversion barrier, through a planar transition state, of only 11 kcal mol^-1. The much more concave structure of 1 than corranulene leads to the greatly increased strain in its all-planar TS. This implies that properly substituted analogues of 1 will be chiral and configurationally stable. Not remarked upon is that the inversion pathway, which will interchange enantiomers when 1 is properly substituted, follows a fully chiral path, as discussed in this post.

1
1TS	1pl

Figure 1. B3LYP/cc-pVDZ optimized geometries of 1, 1TS, and 1pl.

Reference

(1) Wu, T.-C.; Chen, M.-K.; Lee, Y.-W.; Kuo, M.-Y.; Wu, Y.-T. "Bowl-Shaped Fragments of C₇₀ or Higher Fullerenes: Synthesis, Structural Analysis, and Inversion Dynamics," Angew. Chem. Int. Ed. 2013, 52, 1289-1293, DOI: 10.1002/anie.201208200.

InChIs

1: InChI=1S/C38H14/c1-3-17-21-11-7-15-9-13-23-19-5-2-6-20-24-14-10-16-8-12-22-18(4-1)27(17)33-35-29(21)25(15)31(23)37(35)34(28(19)20)38-32(24)26(16)30(22)36(33)38/h1-14H
InChIKey=KLCLRPVBVWXTPN-UHFFFAOYSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.