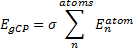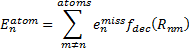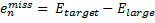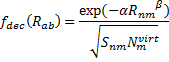Synthesis, Characterization, and Computational Studies of Cycloparaphenylene Dimers

Xia, J.; Golder, M. R.; Foster, M. E.; Wong, B. M.; Jasti, R. J. Am. Chem. Soc. 2012, 134, 19709
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Nanotubes are currently constructed in ways that offer little control of their size and chirality. The recent synthesis of cycloparaphenylenes (CPP) provides some hope that fully controlled synthesis of nanotubes might be possible in the near future. Jasti has now made an important step forward in preparing dimers of CPP such as 1.¹

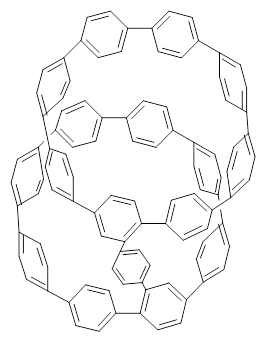1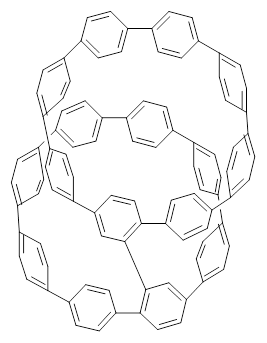

2

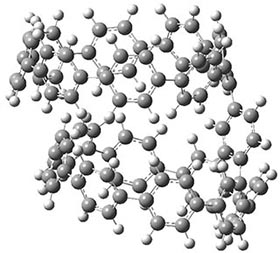
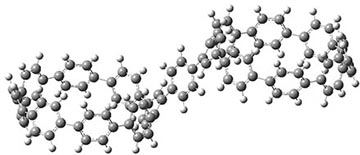
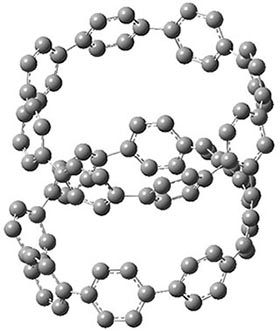
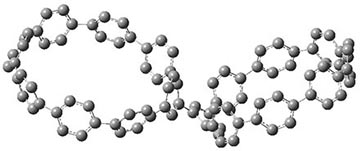
They also performed B3LYP-D/6-31G(d,p) computations on 1 and the directly linked dimer 2. The optimized geometries of these two compounds in their cis and trans conformations are shown in Figure 1. Interestingly, both compounds prefer to be in the cis conformation; cis-1 is 10 kcal mol^-1 more stable than trans-1 and cis-2 is 30 kcal mol^-1 more stable than the trans isomer. While a true transition state interconnecting the two isomers was not located, a series of constrained optimizations to map out a reaction surface suggests that the barrier for 1 is about 13 kcal mol^-1. The authors supply an interesting movie of this pseudo-reaction path (download the movie).

cis-1	trans-1
cis-2	trans-2

Figure 1. B3LYP-D/6-31G(d,p) optimized geometries of the cis and trans conformers of 1 and 2. (Be sure to click on these images to launch a 3-D viewer; these structures come to life in 3-D!)

References

(1) Xia, J.; Golder, M. R.; Foster, M. E.; Wong, B. M.; Jasti, R. "Synthesis, Characterization, and Computational Studies of Cycloparaphenylene Dimers," J. Am. Chem. Soc. 2012, 134, 19709-19715, DOI: 10.1021/ja307373r.

InChIs

1: InChI=1S/C106H82/c1-5-13-79-21-9-17-76-29-37-85(38-30-76)95-59-63-98(64-60-95)103-71-69-101(82(16-8-4)24-12-20-77-27-35-84(36-28-77)90-51-55-94(56-52-90)91-45-41-86(79)42-46-91)73-105(103)99-65-67-100(68-66-99)106-74-102-70-72-104(106)97-61-57-88(58-62-97)81(15-7-3)23-10-18-75-25-33-83(34-26-75)89-49-53-93(54-50-89)92-47-43-87(44-48-92)80(14-6-2)22-11-19-78-31-39-96(102)40-32-78/h5-16,21-74H,1-4,17-20H2/b21-9-,22-11-,23-10-,24-12-,79-13+,80-14+,81-15+,82-16+
InChIKey=WFVBBCVHFBTQRK-VPGVYKRGSA-N

2: InChI=1S/C100H78/c1-5-13-75-21-9-17-72-29-37-81(38-30-72)91-59-63-94(64-60-91)97-67-65-95(78(16-8-4)24-12-20-73-27-35-80(36-28-73)86-51-55-90(56-52-86)87-45-41-82(75)42-46-87)69-99(97)100-70-96-66-68-98(100)93-61-57-84(58-62-93)77(15-7-3)23-10-18-71-25-33-79(34-26-71)85-49-53-89(54-50-85)88-47-43-83(44-48-88)76(14-6-2)22-11-19-74-31-39-92(96)40-32-74/h5-16,21-70H,1-4,17-20H2/b21-9-,22-11-,23-10-,24-12-,75-13+,76-14+,77-15+,78-16+
InChIKey=HOODCSIDKUJYKE-XJQPCHFNSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems

Kruse, H.; Grimme, S. J. Chem. Phys 2012, 136, 154101
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

Basis set superposition error plagues all practical computations. This error results from the use of incomplete basis sets (thus pretty much all computations will suffer from this problem). The primary example of this error is in the formation of a supermolecule AB from the monomers A and B. Superposition occurs when in the computation of the supermolecule, basis functions centered on B are used to supplement the basis set of A, not to describe the bonding or interaction between the two monomers, but simply to better the description of the monomer A itself. Thus, BSSE always serves to increase the binding in the supermolecule. Recently, this concept has been extended to intramolecularBSSE, as discussed in these posts (A and B).

The counterpoise correction proposed by Boys and Bernardi corrects for the superposition by computing the energy of each monomer using the basis sets centered on both monomers, often referred to as ghost orbitals because the functions are used but not the nuclei upon which they are centered. This can overcorrect for superposition but is the only widely utilized approach to treat the problem. A variation on this approach is what has been suggested for the intramolecular
BBSE problem.

A major discouragement for wider use of counterpoise correction is its computational cost. Kruse and Grimme offer a semi-empirical approach that is extremely cost effective and appears to strongly mimic the traditional counterpoise correction.¹

They define the geometric counterpoise scheme (gCP) that provides an energy correction E_gCP that can be added onto the electronic energy. This term is defined as

Eq. (1)

where σ is an empirically fitted scaling term. The atomic contributions are defined as

Eq. (2)

where e^miss are the errors in the energy of an atom with a particular target basis set, relative to the energy with some large basis set:

Eq. (3)

(On a technical matter, the atomic terms are computed in an electric field of 0.6a.u. in order to get some population into higher energy orbitals.) The f_dec term is a decay function that relates to the distance between the atoms (R_nm) and the overlap
(S_nm):

Eq. (4)

where N^virt is the number of virtual orbitals on atom m, and α and β are fit parameters. Lastly, the overlap term comes from the integral of a single Slater orbital with coefficient

ξ = η(ξs + ξp)/2

Eq. (5)

where ξ_s and ξ_p are optimized Slater exponents from extended Huckel theory, and η is the last parameter that needs to be fit.

There are four parameters and these need to be fit for each specific combination of method (functional) and basis set. Kruse and Grimme provide parameters for a number of combinations, and suggest that the parameters devised for B3LYP are suitable for other functionals.

So what is this all good for? They demonstrate that for a broad range of benchmark systems involving weak bonds, the that gCP corrected method coupled with the DFT-D3 dispersion correction provides excellent results, even with B3LYP/6-31G*! This allows one to potentially run a computation on very large systems, like proteins, where large basis sets, like TZP or QZP, would be impossible. In a follow-up paper,² they show that the B3LYP/6-31G*-gCP-D3 computations of a few Diels-Alder reactions and computations of strain energies of fullerenes match up very well with computations performed at significantly higher levels.

Once this gCP method and the D3 correction are fully integrated within popular QM programs, this combined methodology should get some serious attention. Even in the absence of this integration, these energy corrections can be obtained using the web service provided by Grimme at http://www.thch.uni-bonn.de/tc/gcpd3.

References

(1) Kruse, H.; Grimme, S. "A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems," J. Chem. Phys 2012, 136, 154101-154116, DOI: 10.1063/1.3700154

(2) Kruse, H.; Goerigk, L.; Grimme, S. "Why the Standard B3LYP/6-31G* Model Chemistry Should Not Be Used in DFT Calculations of Molecular Thermochemistry: Understanding and Correcting the Problem," J. Org. Chem. 2012, 77, 10824-10834, DOI: 10.1021/jo302156p

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.

FixSol solvation model and FIXPVA2 tessellation scheme

Nandun M. Thellamurege and Hui Li Journal of Chemical Physics 2012 137, 246101 (Paywall)

Contributed by Jan H. Jensen

This paper introduces a variant of the conductor like polarizable continuum model (C-PCM) called FixSol and a modified area tesselation scheme (FIXPVA2) that both serve to increase the numerical stability of geometry optimizations and molecular dynamics simulations.

The C-PCM equation is $${\bf Cq}=-\frac{\varepsilon-1}{\varepsilon}{\bf V}\text{ where } C_{ij}=\frac{1}{r_{ij}}$$Here $r_{ij}$ is the distance between tesserae centers so when atomic spheres and, hence, tesserae points get close the C-PCM equations become numerically unstable.

This has traditionally been dealt with by associating damping functions with each tesserae point (see for example the work by York and Karplus) and FIXPVA2 is a variant of this approach.  However, this study goes even further and modified the $C$ matrix for tesserae that are within a certain cutoff with a smooth transition to C-PCM beyond the cutoff.  The resulting energies are within 0.5 kcal/mol of conventional C-PCM calculations for small molecule ab initio calculations.

However, what really caught my eye was that the demonstration of numerical stability was done by short (10-ps) FixSol-PCM/CHARMM molecular dynamics simulations of a small protein and 13-base pair piece of DNA with energy conservation to within 0.09 kcal/mol.  This is indeed a very stringent text of numerical stability and I don't recall having seeing PCM MD simulations on such large systems, but feel free to correct me in the comments.  Unfortunately timings where not given.

Full disclosure: I was Hui Li's PhD advisor


This work is licensed under a Creative Commons Attribution 3.0 Unported License. 

Graphene-derived nanorings of electronic power

P. V. Avramov, D. G. Fedorov, P. B. Sorokin, S. Sakai, S. Entani, M. Ohtomo, Y. Matsumoto, H. Naramoto, J. Phys. Chem. Lett. 3 (2012) 2003-2008

It is well know that a benzene molecule is highly symmetric. The tale of the rings begins with first making a ribbon, which has only one benzene ring for its width. This, however, still preserves the symmetry between the top and bottom. By either substituting hydrogen atoms on one side or replacing carbon with heteroatoms, one can create a further asymmetry.

 

Electronically, this system has a dipole moment, which forces it to slightly bend forming an arc rather than a straight chain of rings. The result of this subtle asymmetry has been studied for zigzag nanoribbons made from fluorinated graphene, boron nitride and silicon carbide. All of these ribbons have a curvature, mostly in the plane, but the fluorinated graphene also out of plane.

The effect of the subtle curvature disappears in wider ribbons: for ribbons with the width of three rings it is already barely seen.

The electronic properties of these bent ribbons depend on their composition, length and width: some ribbons have a triplet ground state (fluorinated graphene), whereas the HOMO-LUMO gap also varies widely from nearly metallic to semiconductor. A desired gap can be created by modifying the size and composition.

Finally, if one extends a bent ribbon long enough, eventually it closes into a full ring, or one can make an incomplete ring. In order to optimize the geometry of a full BN nanoring having the diameter of 105 nm and composed of 1312 aromatic BN rings, the fragment molecular orbital method was used, which is capable of performing ab initio type of calculations of large molecular systems.The lord of the nanorings forged three rings made of 1311, 1312 and 1313 BN rings, whose geometry was fully optimized to verify that they are not distorted. 

The full rings are found to have a nearly zero dipole moment, as follows from symmetry. However, incomplete rings have a huge dipole moment, for example, the ring with a 120 degree opening has a dipole moment of 493 Debye.

These results are obtained from DFT calculations. It the literature one can find many reports on wide ribbons, but no experiment on narrow ribbons has been reported so far to the best of my knowledge.

 

Extreme oxatriquinanes and a record C–O bond length

Gunbas, G.; Hafezi, N.; Sheppard, W. L.; Olmstead, M. M.; Stoyanova, I. V.; Tham, F. S.; Meyer, M. P.; Mascal, M. Nat. Chem. 2012, 4, 1018
Contributed by Steven Bachrach.
Reposted from Computational Organic Chemistry with permission

I have written a number of posts discussing long C-C bonds (here and here). What about very long bonds between carbon and a heteroatom? Well, Mascal and co-workers¹ have computed the structures of some oxonium cations that express some very long C-O bonds. The champion, computed at MP2/6-31+G**, is the oxatriquinane 1, whose C-O bond is predicted to be 1.602 Å! (It is rather disappointing that the optimized structures are not included in the supporting materials!) The long bond is attributed not to dispersion forces, as in the very long C-C bonds (see the other posts), but rather to σ(C-H) or σ(C-C) donation into the σ*(C-O) orbital.

1

Inspired by these computations, they went ahead and synthesized 1 and some related species. They were able to get crystals of 1 as a (CHB₁₁Cl₁₁)^- salt. The experimental C-O bond lengths for the x-ray crystal study are 1.591, 1.593, and 1.622 Å, confirming the computational prediction of long C-O bonds.

As an aside, they also noted many examples of very long C-O distances within the Cambridge
Structural database that are erroneous – a cautionary note to anyone making use of this database to identify unusual structures.

References

(1) Gunbas, G.; Hafezi, N.; Sheppard, W. L.; Olmstead, M. M.; Stoyanova, I. V.; Tham, F. S.; Meyer, M. P.; Mascal, M. "Extreme oxatriquinanes and a record C–O bond length," Nat. Chem. 2012, 4, 1018-1023, DOI: 10.1038/nchem.1502

InChIs

1: InChI=1S/C21H39O/c1-16(2,3)19-10-12-20(17(4,5)6)14-15-21(13-11-19,22(19)20)18(7,8)9/h10-15H2,1-9H3/q+1/t19-,20+,21-
InChIKey=VTBHIDVLNISMTR-WKCHPHFGSA-N

This work is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.